Sources: Article du Monde en ligne du 07 mars 2020
Chiffres issus du site internet de John Hopkins University (Coronavirus live map)
Cours de Modélisation Mathématique du Pr. J-Y Mérindol (ULP, Strasbourg 1er semestre, 1ère année, 1989)
En lisant l’article du monde présentant l’évolution temporelle des cas recensés de Coronavirus dans divers pays (dont l’Italie et la France), je me suis demandé s’il était possible de réaliser un modèle mathématique simple pouvant donner des estimations ou, du moins, des tendances quant à l’épidémie de Coronavirus.
Or, dans le cours de Modélisation Mathématique cité dans les sources, le Professeur Mérindol avait exposé le modèle S-I-R (Sane- Infected- Recovered) qui est une modélisation très simplifié d’une épidémie. Ce modèle se base sur la théorie des équations différentielles ordinaires du 1er ordre et sur une loi de type d’action de masse.
Une équation différentielle est une équation dont l’inconnue n’est plus un nombre mais une fonction faisant intervenir les dérivées de celle-ci. L’équation est dite du 1er ordre lorsque n’apparaissent que la fonction et sa dérivée première dans son expression.
Une loi d’action de masse est une expression reliant les réactifs et les réactants menant à un équilibre réactionnel.
1- Un modèle extrêmement simplifié:
Dans un 1er temps, nous n’allons que considérer les évolutions temporelles de la population saine S(t), de la population infectée I(t) et de la population guérie R(t):
le modèle proposé est alors un modèle S-I-R pouvant être décrit par le système d’équations suivant:
(i): S'(t) = -B*I(t)*S(t)
(ii): I'(t) = B*I(t)*S(t) - g*I(t)
(iii): R'(t) = g*I(t)
L’équation (i) correspond à la diminution de la population saine. Celle-ci diminue à chaque fois que ses membres sont en contact avec des personnes infectées.
Symétriquement, l’équation (ii) correspond à l’augmentation des personnes infectées lorsque celles-ci sont en contact avec des gens sains mais elle diminue du nombre de personnes guéries.
Finalement, la troisième équation correspond à l’augmentation de la population guérissant de la maladie.
On observe que S'(t)+I’(t)+R'(t) = 0. Ainsi, S(t)+I(t)+R(t) est une valeur constante. Cette constante étant la taille de la population totale, soit, pour le cas français, 67 000 000.
Le paramètre B correspond au taux de contagion.
Le paramètre g correspond au taux de guérison.
La difficulté consiste à déterminer la valeur des paramètres B et g. En effet, les données sont pratiquement inexistantes et peu fiables.
Or, il a été souvent dit qu’une personne infectée en contaminait trois. Cependant, cela ne veut pas dire que la progression est une suite géométrique de raison q = 3 (sinon, l’ensemble de la population mondiale serait déjà infectée) mais que sur l’ensemble des personnes qu’un malade va rencontrer, il en infectera 3. A titre d’exemple , si cette personne rencontre une centaine de personnes, il en infectera 3, soit 3%. Au cas particulier, B a été choisi égal à 1.03/N, N étant la population totale.
Compte-tenu des éléments fournis par John Hopkins University, le paramètre g a été choisi comme étant égal à 0.0183.
Bien que ce système se résolve simplement, il est plus intéressant d’utiliser l’esclave de silicium pour faire une simulation numérique.
L’ordinateur utilisé est un misérable centrino fonctionnant sous Linux, distribution Lubuntu (ben oui, c’est un papi et je suis contre le gaspillage), le langage de programmation est Python 3.6.9 ( parce que tout est plus facile en Python).
La méthode employé est un schéma d’Euler explicite à un pas (oui bon, je reconnais, ça a été fait à l’arrache ). Ce schéma est connu pour être peu précis.
Les données initiales sont:
S(0) = N = 67 000 000
I(0) = 1
R(0) = 0
B= 1.03/N
g= 0.0183
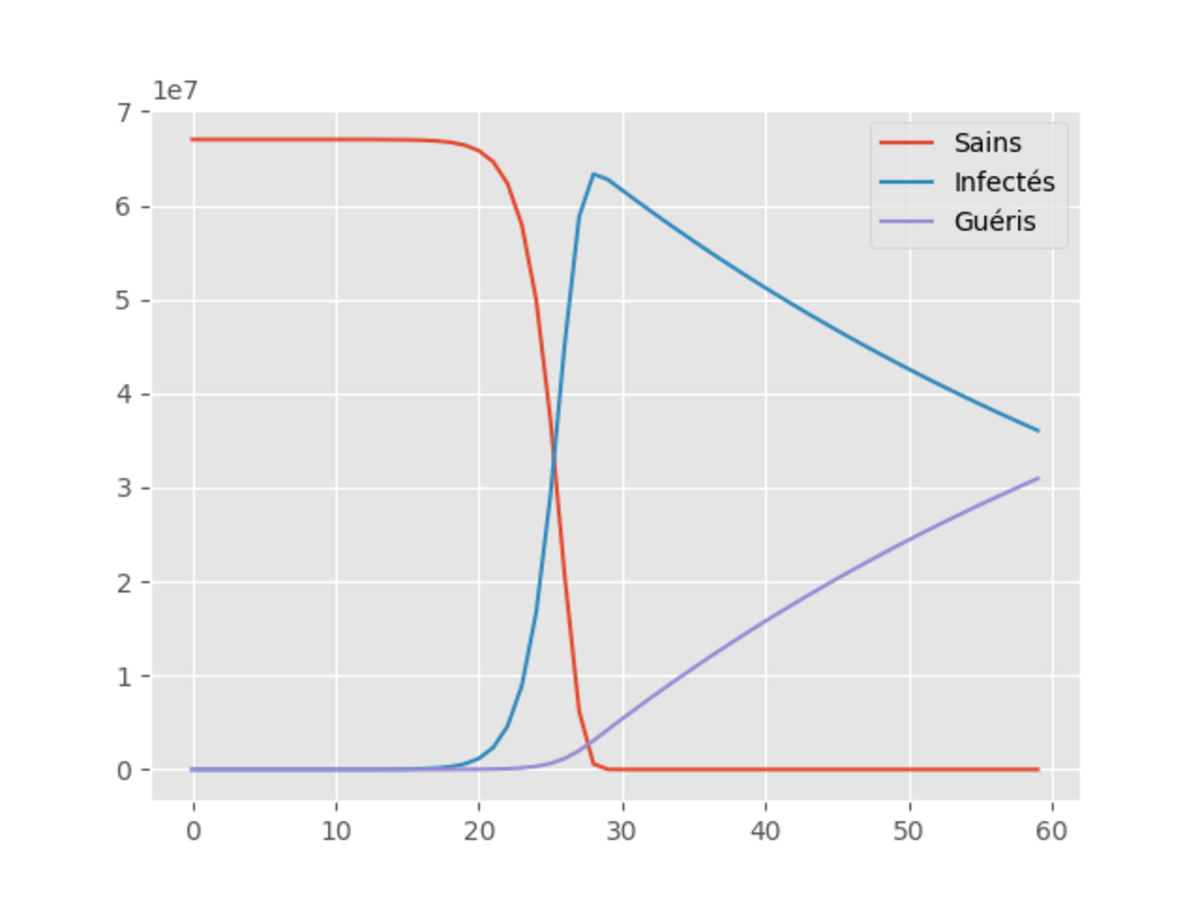
Agrandissement : Illustration 1
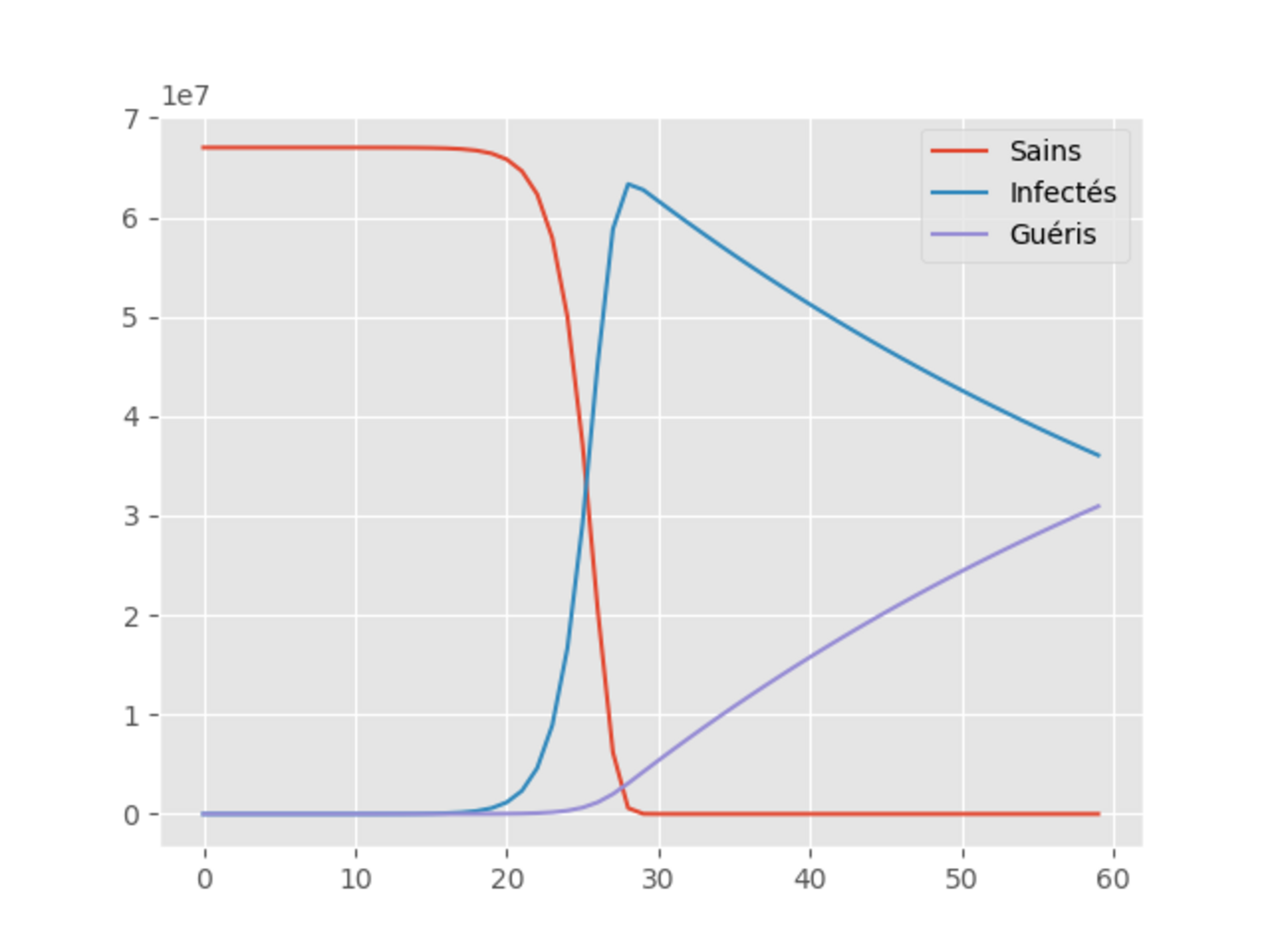
L’ordonnée nous donne le nombre de personnes, l’abcisse étant les jours. On constate déjà, qu’avec ce modèle, pratiquement l’ensemble de la population française est infectée après seulement 25 jours.
Affinons le modèle, en prenant en compte les morts provoqués par l’épidémie:
Au modèle S-I-R précédent, on rajoute une équation déterminant l’augmentation du nombre de morts. Le taux de mortalité choisi est d = 0.0113. Ce chiffre a été déterminé en utilisant les données de John Hopkins University, notamment les données sud-coréenne qui paraissent être les plus fiables compte-tenu de leur politique de détection massive de la population.
Ainsi, il faut corriger l’équation (ii) en y soustrayant le terme d*I(t) qui traduit le nombre de personnes infectées qui sont mortes et donc qui ne peuvent plus infecter qui que soit et symétriquement une nouvelle équation est introduite:
(iv) D’(t)= d*I(t)
Celle-ci traduit le nombre de personnes infectées mourant de la maladie.
Fouettons l’esclave et regardons religieusement les courbes qu’il nous crache avec cette hypothèse supplémentaire:
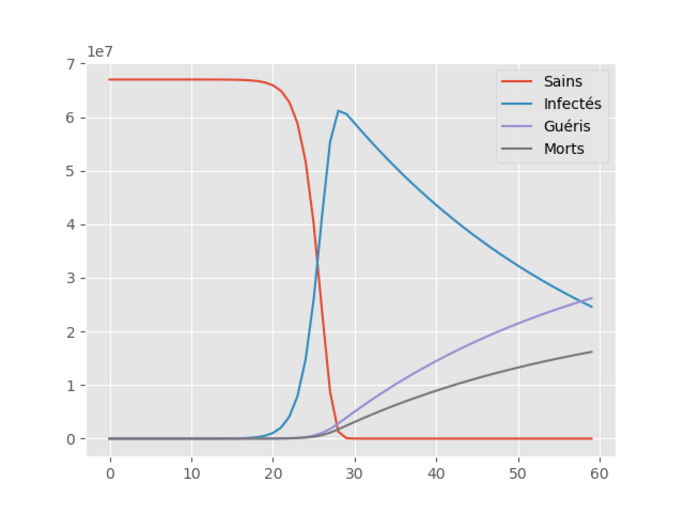
Agrandissement : Illustration 2
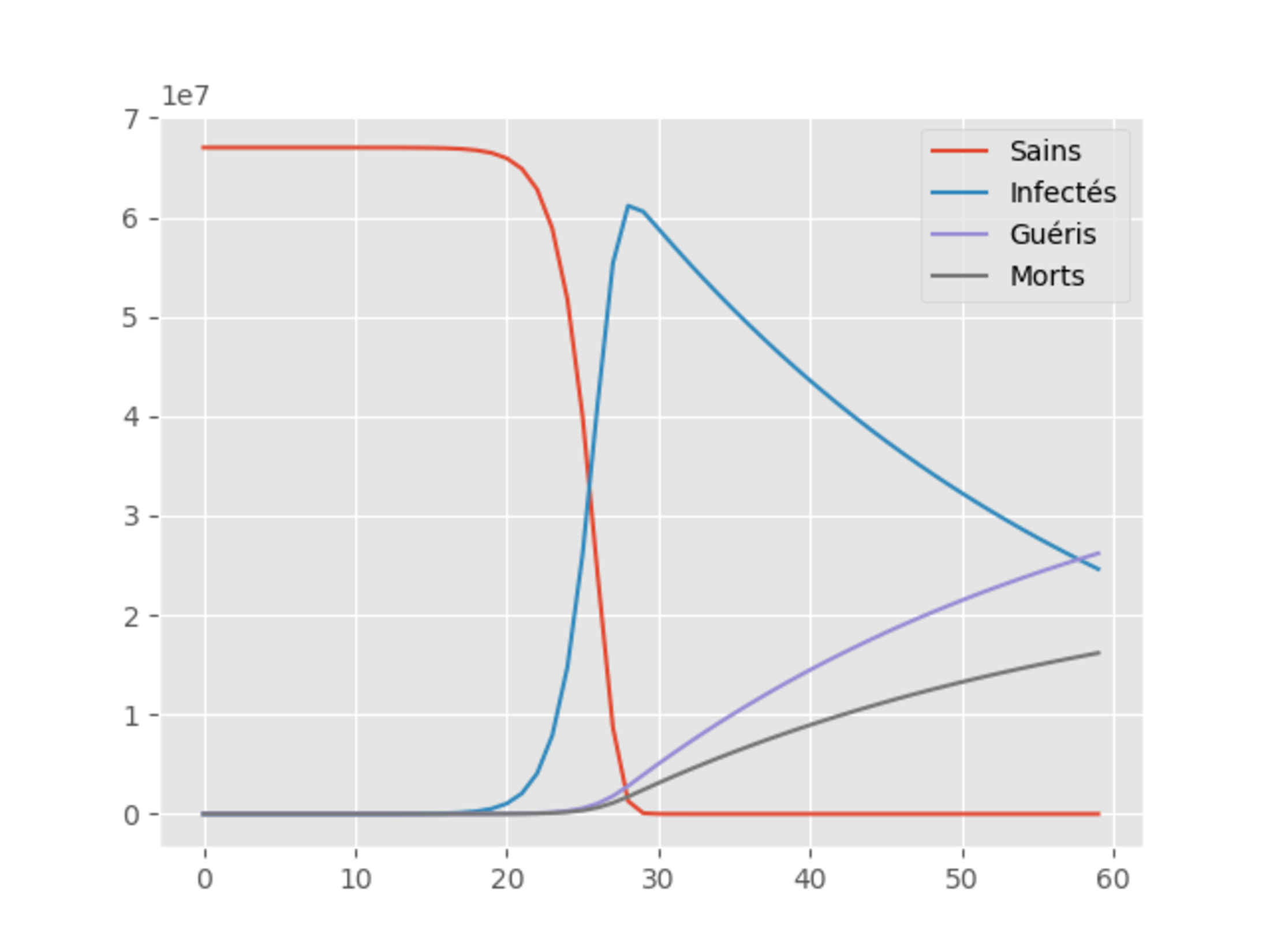
L’abcisse et l’ordonnée représente toujours respectivement les jours et les populations.
La conclusion qui s’impose est que la situation est catastrophique mais ceci n’est qu’un modèle, extrêmement simplifié, fort heureusement.
2- Imaginons différents scénarios:
a- Confinement de la population:
Supposons que les pouvoirs publics décident d’une politique de confinement au détriment d’une politique de détection et de mise en quarantaine des malades. Tout lien avec les politiques réelles étant bien évidemment de l’ordre de la Science-Fiction, nous savons tous que notre illustre gouvernement a merveilleusement bien anticipé la situation.
Traduire une politique de confinement revient à faire varier le paramètre B de la section précédente.
En interrogeant l’oracle de silicium, il a daigné me communiquer les courbes suivantes:
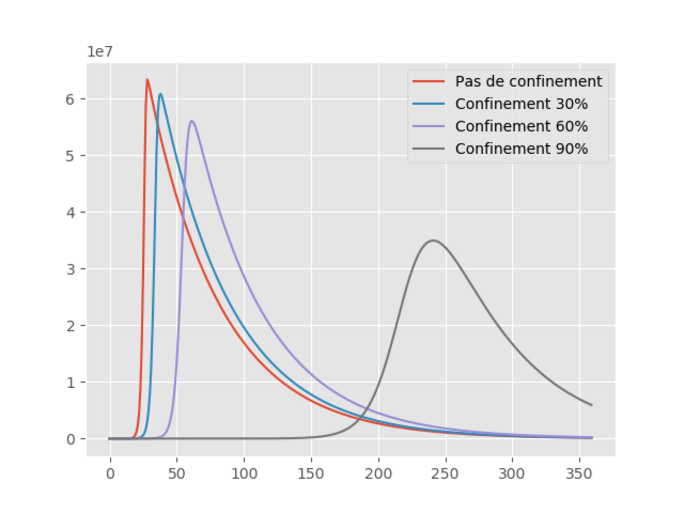
Agrandissement : Illustration 3
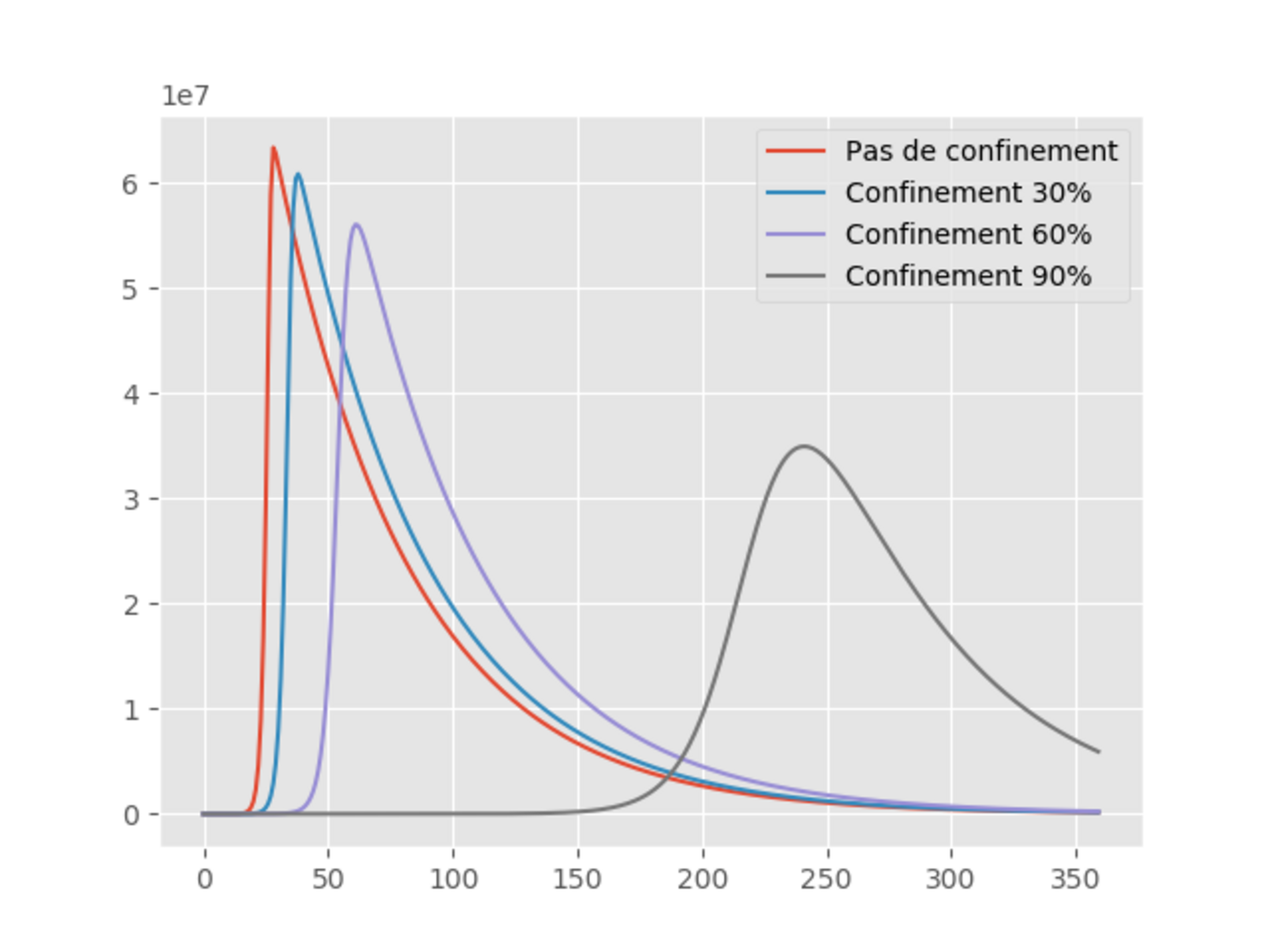
L’abcisse et l’ordonnée représentent respectivement les jours et les populations. La conclusion qui s’impose est qu’à moins d’un confinement brutal de l’ordre de 90%, i.e, on ne voit que les personnes vivant sous le même toit, cette politique est vouée à l’échec, car d’une part, hormis le dernier cas, le nombre de contaminés est toujours supérieur à cinquante millions (50 000 000). D’autre part, le pic de contamination se déplace légèrement dans le temps, sauf pour le confinement total, oû le pic intervient 6 mois plus tard, mais on est encore à plus de trente millions de contaminés.
En résumé, la politique de confinement est quelque peu douteuse.
b- Si le confinement ne fonctionne pas , quid d’une politique de détection?
Posons nous la question de la pertinence d’une politique de détection à l’instar de nos amis coréens.
Au système d’équations différentielles précédent, il faut rajouter une équation différentielle traduisant la détection et la mise en quarantaine du sujet infecté. Celle-ci est assez évidente et est de la forme:
(v) Q’(t) = f*I(t)
Il ne faut pas oublier alors de soustraire dans l’équation (ii) le terme f*I(t).
Le terme f est le terme de détection, celui-ci est strictement positif et strictement inférieur à 1, soit 0<f<1. On ne peut détecter plus d’infectés qu’il y en a.
Relançons la machine et regardons les jolies courbes:
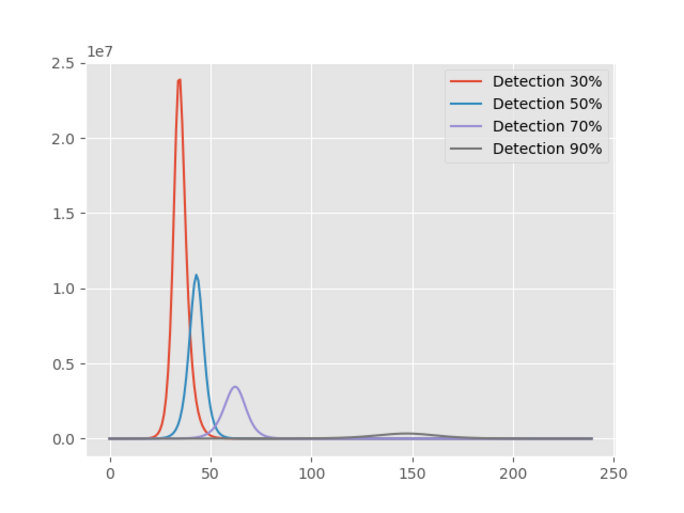
Agrandissement : Illustration 4
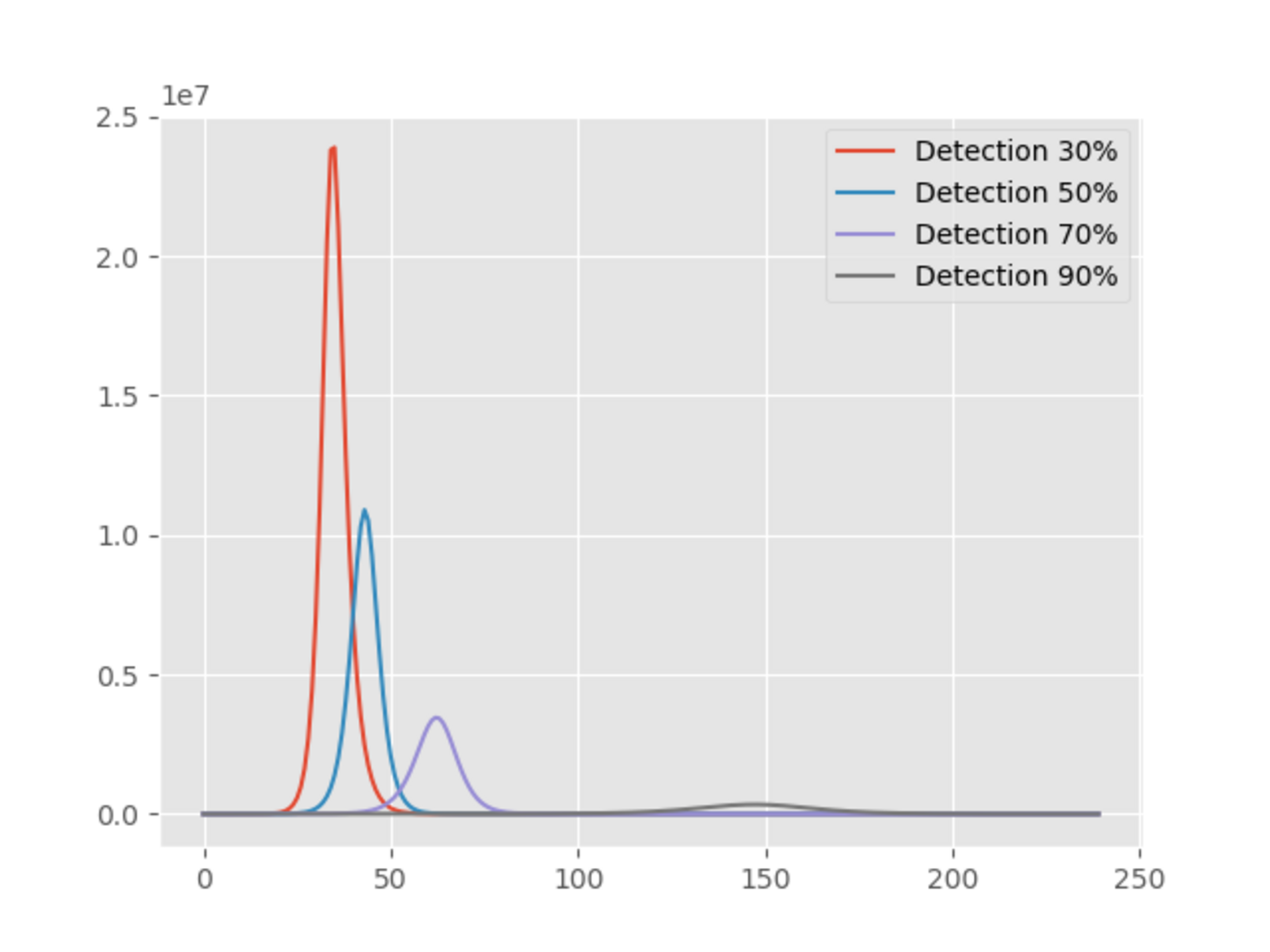
La première conclusion est que, par rapport à la politique de confinement, la politique de détection et de mise en quarantaine paraît efficace. En effet, avec un taux de détection de 30%, la population de personnes infectées est inférieure à 24 000 000 et plus le taux augmente, moins il y aura de personnes infectées. Cependant, regardons plus en détail la courbe correspondant à un taux de détection de 90%:
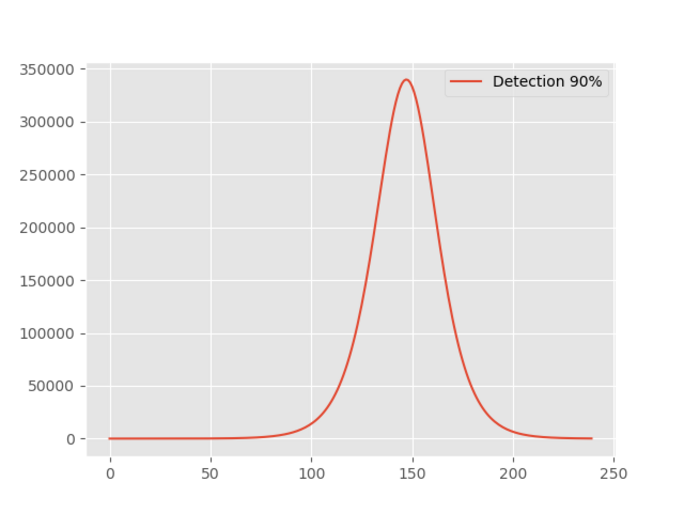
Agrandissement : Illustration 5
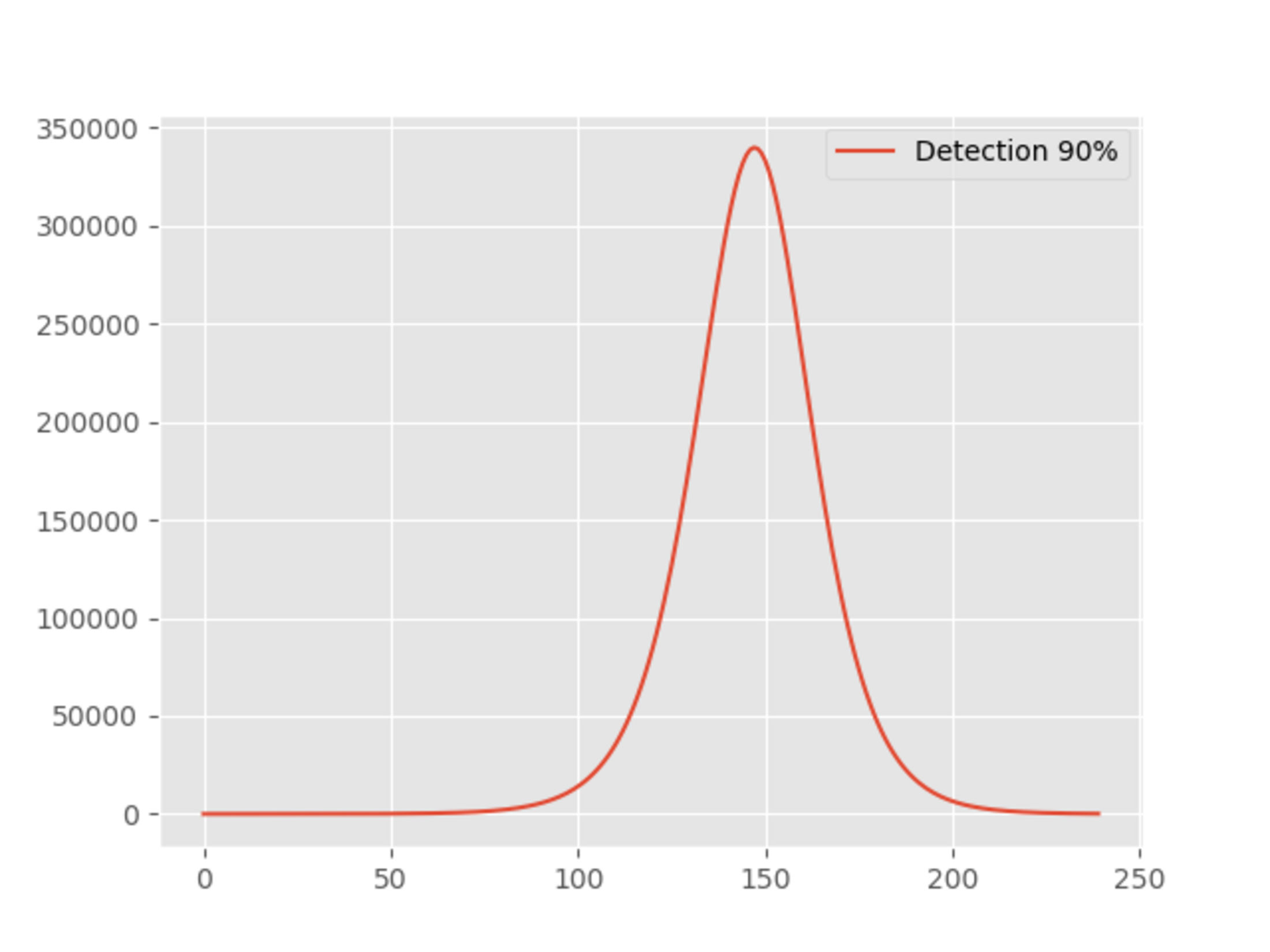
La conclusion est sans appel, moins de 350 000 contaminés.
A ce stade, faut-il encore conclure? Visiblement, la politique de détection systématique est d’une efficacité redoutable, contrairement à une politique de confinement.
La stratégie des coréens est donc la bonne.
c- Encore un dernier petit scénario pour la route:
Supposons que les pouvoirs publics aient rapidement pris la mesure de ce qui arrivait malgré la casse systématique du système de santé au nom du sacro-saint bilan comptable.
Le gouvernement a correctement identifié la stratégie à mettre en place et a donc combiné la détection systématique (80%)et le confinement. Par contre, pour mettre la politique de détection en place, il lui a fallu quelques semaines.Cependant, au bout de 70 jours, la détection tombe à 40% avant de remonter jusqu’à 64%, ceci ne traduisant certainement pas les politiques d’austérité (tu parles). Au bout de 90 jours, il arrive de nouveau à détecter jusqu’à 64% des cas.
Au bout de 140 jours, ne détectant plus de nouveau cas, le gouvernement décide qu’il n’est plus nécessaire de tester systématiquement la population et nous sommes de nouveau dans la politique du Business as usual.
Interrogeons une dernière fois la Bête. Que nous dit-elle?
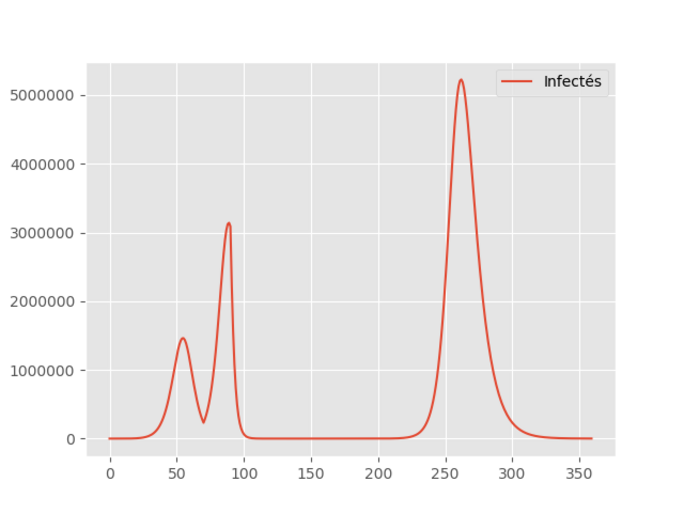
Agrandissement : Illustration 6
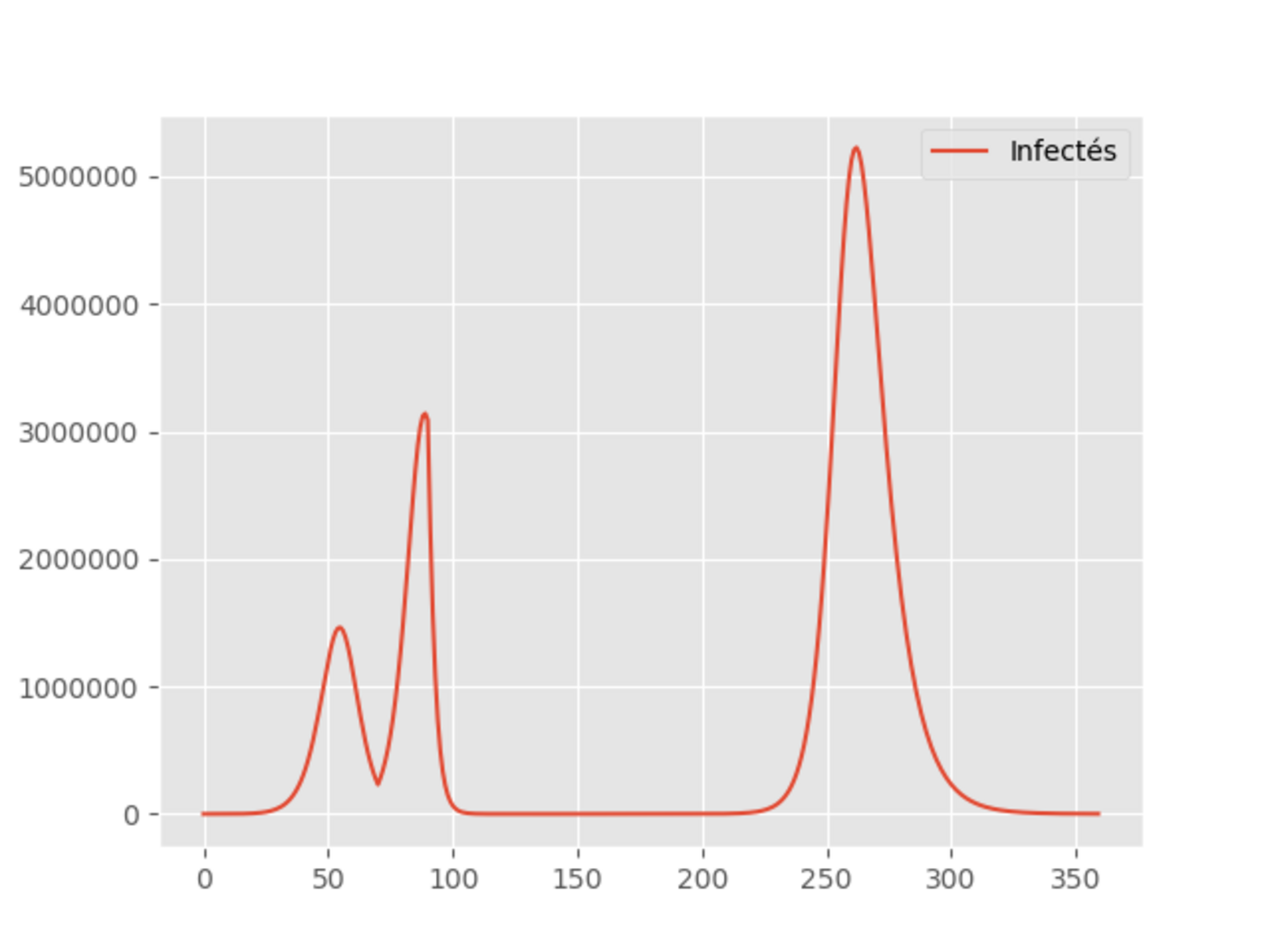
Le fait que, dans un premier temps, le nombre de contaminés soit supérieur à un million traduit le temps de mis en oeuvre de la politique de détection qui donne des résultats assez rapidement. Cependant, le système est surchargé et donc les chiffres montent à 3 millions, mais le gouvernement arrive à anticiper à nouveau correctement et le nombre de nouveaux contaminés baisse rapidement.
Malheureusement, le gouvernement s’étant félicité de son excellente gestion de crise pense pouvoir continuer là oû il s’était arrêté avant la crise du Coronavirus. Pas de chance! La 2ème vague arrive près de 6 mois plus tard...
Conclusion:
Le modèle exposé présente beaucoup de faiblesses puisque que beaucoup d’hypothèses simplificatrices ont été supposées, à savoir utiliser une simple loi d’action de masse et peu de paramètres. Par ailleurs la détermination de ces derniers peut être discutable, compte-tenu du peu d’informations pertinentes à disposition. De plus, l’algorithme employé pour les simulations numériques n’est pas des plus précis.
Le modèle pourrait être combiné avec des outils probabilistiques tels que les méthodes de Monte-Carlo oû les matrices densité.
Par ailleurs, la population a été considérée comme un bloc monolithique, alors qu’on pouvait considérer les différentes tranches d’âge, les modes de vie (urbain ou rural) et les connexions en réseau du pays.
Cependant, le modèle donne des tendances intéressantes, notamment sur ce qui fonctionne et ce qui ne fonctionne pas.
Il faut aussi préciser que les valeurs numériques ( que je n’ai pas exposées ici) sont proches à 8% près de la réalité du moins jusqu’à dimanche dernier. Je n’ai pas vérifié depuis, la précision obtenue m’ayant complètement déprimé.
Ce qui est particulièrement inquiétant et donne néanmoins une certaine valeur à ce modèle, c’est qu’il démontre que la politique de gestion des coréens est la plus efficace et surtout l’impréparation, l’improvisation et l’incurie de ceux qui nous gouvernent.
Je précise que je ne suis pas épidémiologiste et que ce modèle a été élaboré un samedi après-midi avec des outils élémentaires de mathématiques au fin fond de la Moselle-est parce que je n’avais rien d’autre à faire à ce moment.
Je ne peux croire que notre gouvernement, avec toutes les informations à disposition, entourés d’experts qui ont des outils autrement plus efficaces que quelques pauvres équations différentielles soit à ce point médiocre dans la gestion de cette crise.
A vrai dire les mots me manquent.



