L’homme et la femme ont tous deux un organe extraordinaire, le même organe : l’oreille.
L’oreille est l’organe récepteur de l’un de nos cinq sens, le sens qui nous permet de nous entendre.
- C’est anodin, trivial, c’est quoi cette banalité ! Un bon mot ? …, dit-elle.
- Oui, c’est anodin, … c’est grâce à l’oreille, répond-il.
Agrandissement : Illustration 1
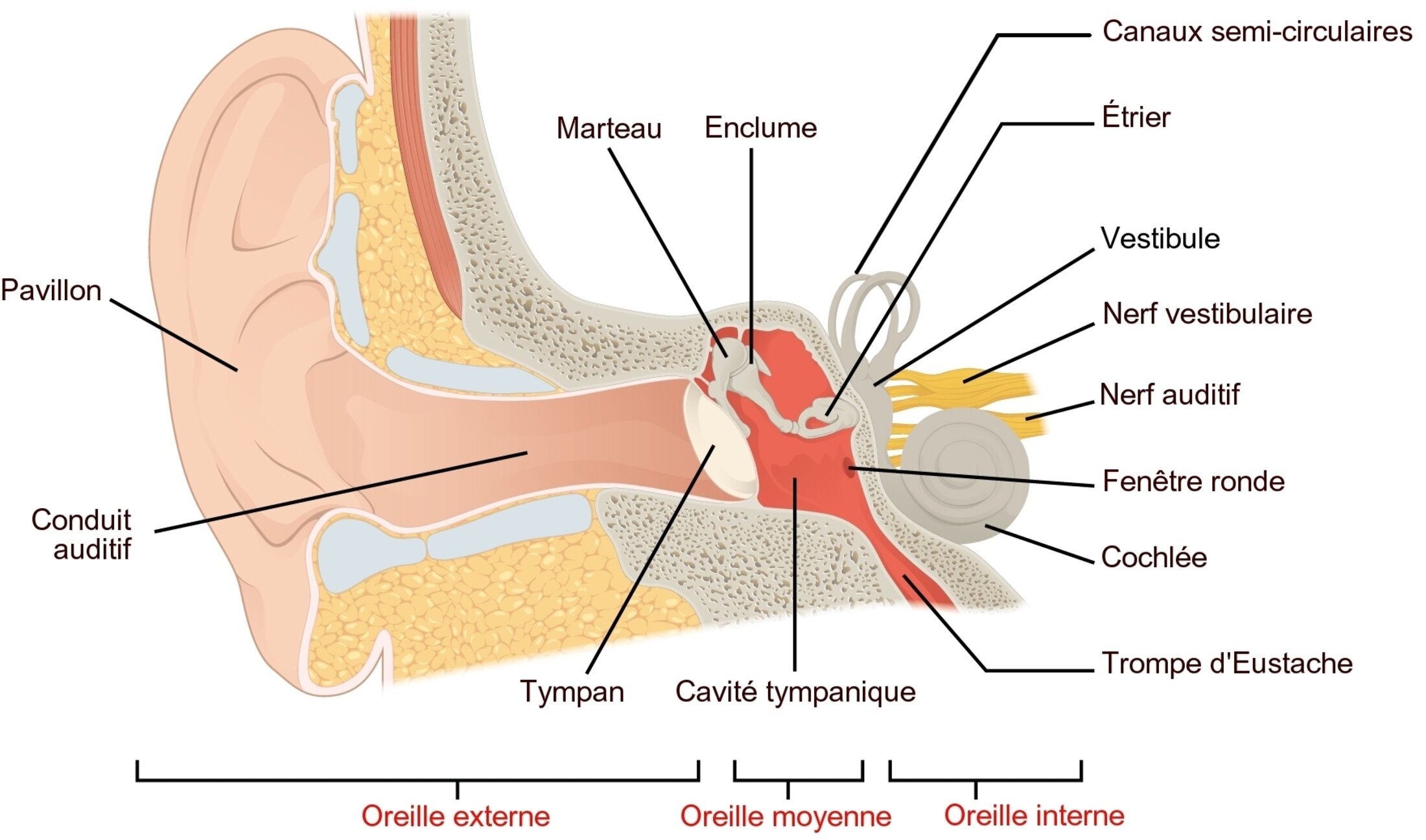
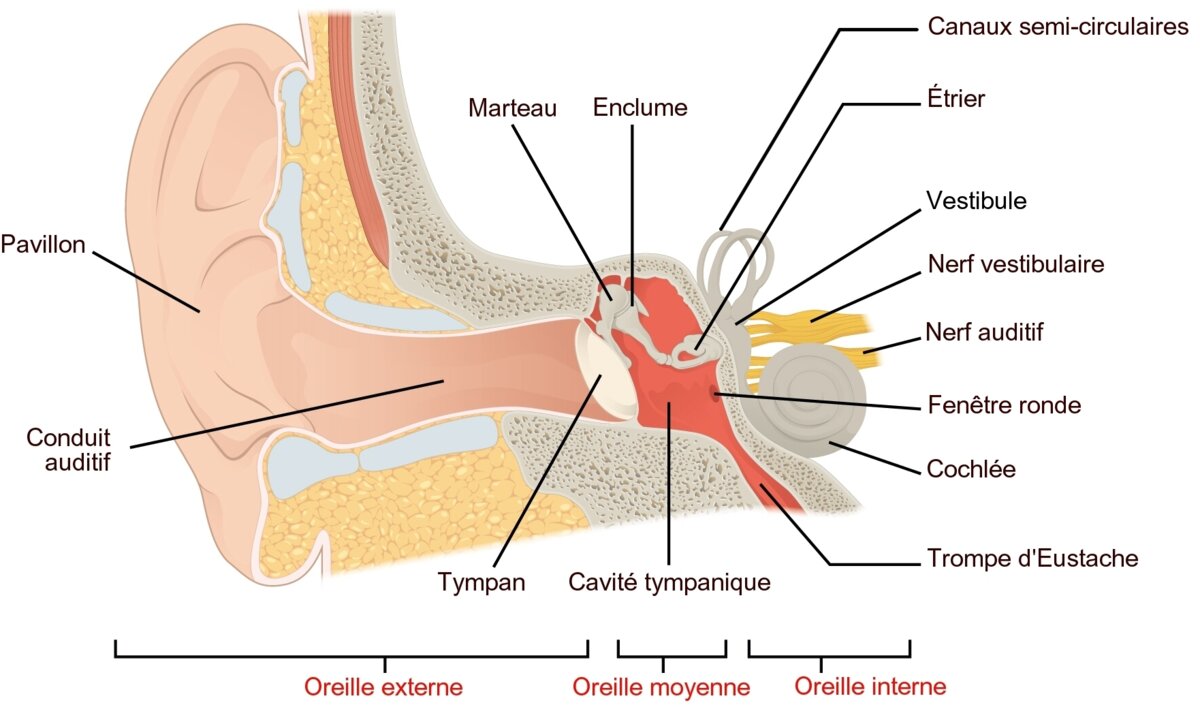
Beaucoup connaissent «sommairement» (mais c’est bien suffisant) le fonctionnement de l’oreille, le tympan comme une peau de tambour, sensible aux vibrations de l’air porteuses du signal sonore, qui actionne des osselets pour transmettre le signal à l’oreille interne, lieu de transformation de la vibration mécanique en signal électrique pour le nerf auditif.
Je me souviens de cette leçon « sommaire » découverte à l’école primaire ou au collège.
J’ai eu la chance de m’épanouir dans des études scientifiques, plutôt mathématiques et mécaniques. Des études modestes mais grâce auxquelles j’ai découvert, entre autre, la magie du logarithme. Le logarithme, ce mot impalpable avec lequel on ne sait jamais où poser le « h ». Quel rapport avec l’oreille me direz-vous ? Patience. Mais je vois au fond certains qui ont déjà compris.
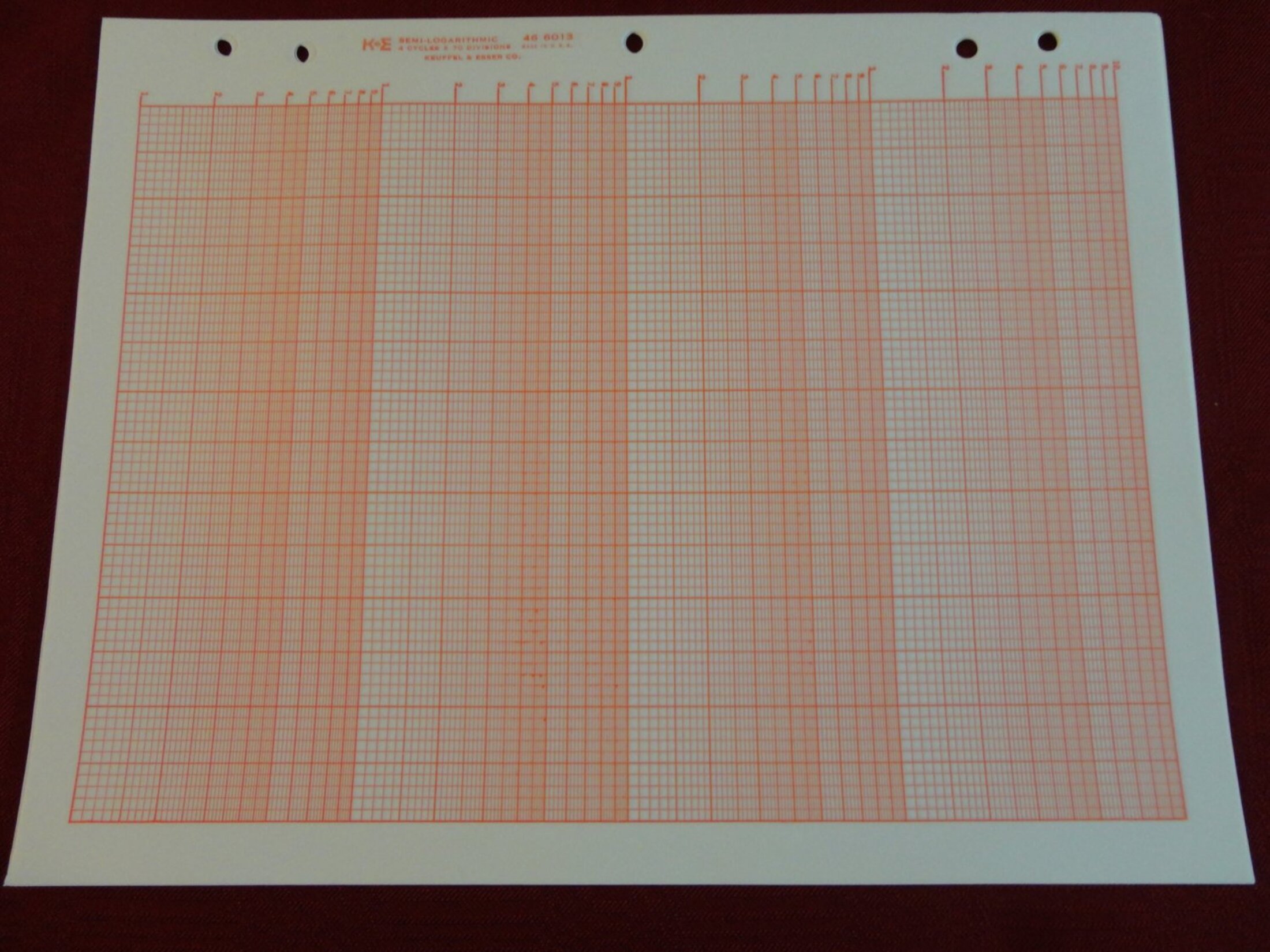
À l ‘école, j’ai d’abord découvert le logarithme par son papier : le papier logarithmique. Un papier couvert d’une grille imprimée dont les espaces entre les lignes sont variables, une grille qui permet, en physique, de tracer des courbes de mesures en faisant tenir tous les points de la courbe sur une même feuille. J’étais comme vous, je ne comprenais pas bien pourquoi, mais mon professeur de physique nous disait de faire nos courbes avec ça pour que tous les points tiennent sur la feuille, alors je faisais comme ça. Et ça marchait.
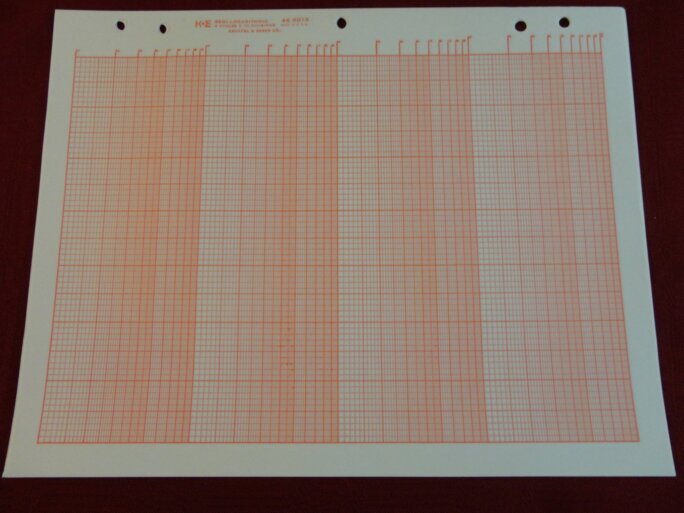
Agrandissement : Illustration 2
Ensuite j’ai entendu parler du logarithme en cours de mathématiques. Enfin pour moi ce terme allait prendre du sens. Et quel sens !
Le logarithme est la fonction primitive de la fonction inverse…
Oui vous voyez, ce n’est pas gagné pour tout le monde… N’ayez crainte. On peut dire aussi que si je dérive le logarithme, j’obtiens la fonction inverse, la fonction 1/x … Pas gagné non plus.
Mais vous savez, quand on est jeune, on a le cerveau mou. On accepte facilement les choses sans les comprendre. Parce qu’on a entendu depuis tout petit qu’on comprendra quand on sera plus grand. Parce qu’il faut faire confiance, et je sais, pour l’avoir vécu, que ce n’est pas toujours facile à vivre. Tant pis, je continue.
Les mathématiques ont cette puissance qu’elles ne sont pas morales, elles ne sont pas politiques, elles n’ont pas d’avis. Elles sont. Et nous, humains, nous essayons de les découvrir en les construisant. Si nous nous trompons, elles se cassent la figure, sans jugement, il n’y a ni bien, ni mal, alors nous recommençons ; ne restera toujours en final de nos constructions en perpétuel croissance, que ce qui est mathématique.
De fait, il n’y a aucun risque à prendre pour argent comptant ce que nous dit le ou la professeur.e de mathématique. S’il ou elle se trompe, un jour nous le découvrirons, s’il ou elle ne se trompe pas, un jour nous comprendrons, car la joie des mathématiques, c’est aussi qu’avec le temps nous comprenons toujours mieux, toujours plus et l’ignorance peut nous accompagner sans danger, nous nous en débarrasserons naturellement avec le temps. Je dirais même que l’ignorance peut nous nourrir à faire des mathématiques. « Tu comprendras quand tu seras grand ».
À ce stade, je ne vois pas en quoi ce logarithme peut m’aider à vivre, si ce n’est vivre en me creusant les méninges, ce qui, pour moi, je l’avoue, est un agréable passe-temps, voire un carburant.
En mathématiques, une fois qu’un outil est à disposition, ici le logarithme, on a le droit de jouer avec. C’est en jouant avec le logarithme que l’on découvre enfin sa raison d’être.
Le logarithme transforme le produit en somme.
Le logarithme transforme la multiplication en addition … M’ouais !
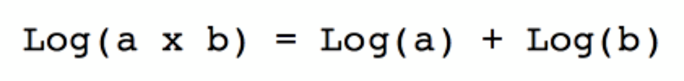
Quand je pense aux difficultés que rencontre ma fille à apprendre par cœur « ses » tables de multiplication… Mais pour elle, les tables d’addition ne sont pas plus faciles. Alors quoi, quel intérêt ? Transformer un produit en somme? Qu’est-ce que ça veut dire ?
Déjà, ça veut dire, comme le disait mon professeur de physique, que l’on peut mettre tout le monde sur la même feuille ; ça marche !
Transformer un produit en somme, ça veut dire que si quelque chose est multiplié par 2, passé au filtre du logarithme, il n’apparaîtra plus comme multiplié par 2 mais augmenté de +2 ... La bonne affaire.
Pour comprendre, rien de tel qu'une bonne séance de ...
Travaux Pratiques (TP pour les intimes).
Imaginons des enfants qui jouent à chat dans la cour de récréation. Supposons qu’il y ait dans le groupe des enfants capables de courir à une vitesse, et des enfants, plus forts physiquement, capables de courir 2 fois plus vite. Oui, on fait souvent ça en mathématiques, des hypothèses bizarres qui n’arrivent jamais dans la vraie vie, mais ça aide à réfléchir.
Rapidement notre groupe d’enfants va se scinder en deux groupes qui évolueront comme deux univers parallèles, homothétiques mais distants. Les enfants qui courent 2 fois plus vite auront la possibilité d'une vie hors du champ du visible des enfants qui courent moins vite. Si, à ce jeu, nous appliquons un filtre logarithmique sur les déplacements, l’enfant qui court 2 fois plus vite n’ira pas deux fois plus loin qu’un enfant qui court moins vite. Si en distance linéaire l’enfant qui court vite se trouve à 1 km, en distance logarithmique, il sera à 6m90. L’enfant qui se trouverait à 2 km linéaires, il serait perçu à 7m60 en distance logarithmique. En logarithmique, il n'y aura pas 1 km entre les enfants, mais 70cm.
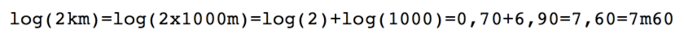
Agrandissement : Illustration 4
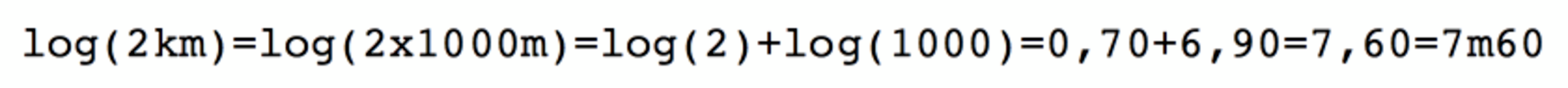
Ceci nous permet de comprendre que le pouvoir de convertir le produit en somme permet de limiter les éloignements tout en conservant les vitesses de chaque enfant et tout en respectant des écarts de distance. Ainsi, le groupe est moins distendu, les enfants resteront plus longtemps ensembles, ils auront plus facilement le temps de changer les règles du jeu pour corriger l’effet néfaste de la dislocation du groupe ou l’effet pervers de l’enfant qui ne peut jamais gagner ou jamais perdre. Parce que si l’enfant ne peut jamais gagner, ou jamais perdre, il se lasse très vite, il arrête de jouer. Au mieux il se rebelle, au pire il disparait.
On me dit à l’oreille, « Quel rapport avec l’oreille ? ».
Oui, j’y viens. Mais je vois qu’il y a des spécialistes qui ont déjà compris (certainement ceux qui savent courir 2 fois plus vite).
L’oreille externe, autrement dit la feuille de chou que nous avons de part et d’autre du crâne, a grosso modo une forme de coquille d’escargot. Si vous essayez de réduire cette forme à une équation mathématique, j’en conviens qu’il faut avoir l’esprit tordu, mais si vous le faites quand même, parce que vous ne pouvez pas vous en empêcher, vous pourrez le faire grâce à la fonction … logarithme. L’oreille externe est une forme (approximative) de fonctions logarithmiques savamment assemblées, une des formes génériques les plus simples étant la coquille d’escargot.
Ah ! On y est.
Si vous êtes un son et que vous plongez dans l’oreille, vous serez chahutée en rebondissant sur les parois de cette feuille de chou en forme de coquille qui vous conduira inexorablement sur le tympan. En faisant vibrer le tympan, vous déclencherez le mouvement d’un marteau qui tape sur une enclume elle-même reliée à un étrier. Ce sont nos osselets vus à l’école primaire. La forme logarithmique du pavillon de l’oreille externe a permis aux sons les plus forts et aux sons les moins forts, aux sons les plus aigus et aux sons les plus graves, de converger vers le même périmètre restreint du tympan tout en restant très bien différenciés les uns des autres, chacun rebondissant sur les parois à sa façon, en fonction de ses propriétés. Ceci est le premier effet logarithmique de l’oreille : rassembler en un lieu restreint tous les sons sans les confondre, quelque soit leur force, quelque soit leur nature, en les préservant.
Mais le jeu du logarithme dans l'oreille ne s’arrête pas là.
Passés les osselets, les sons, traduits en rythmes de tambour, se présentent à l’oreille interne, en particulier à l’entrée d’une deuxième coquille d’escargot : la cochlée.
La cochlée, de forme logarithmique, est enduite de cellules qui sous l’effet des vibrations mécaniques libèrent du glutamate dans les fibres du nerf auditif. Le glutamate est le neuromédiateur du nerf auditif. C’est lui qui permet le voyage du signal jusqu’au cerveau.

Agrandissement : Illustration 5
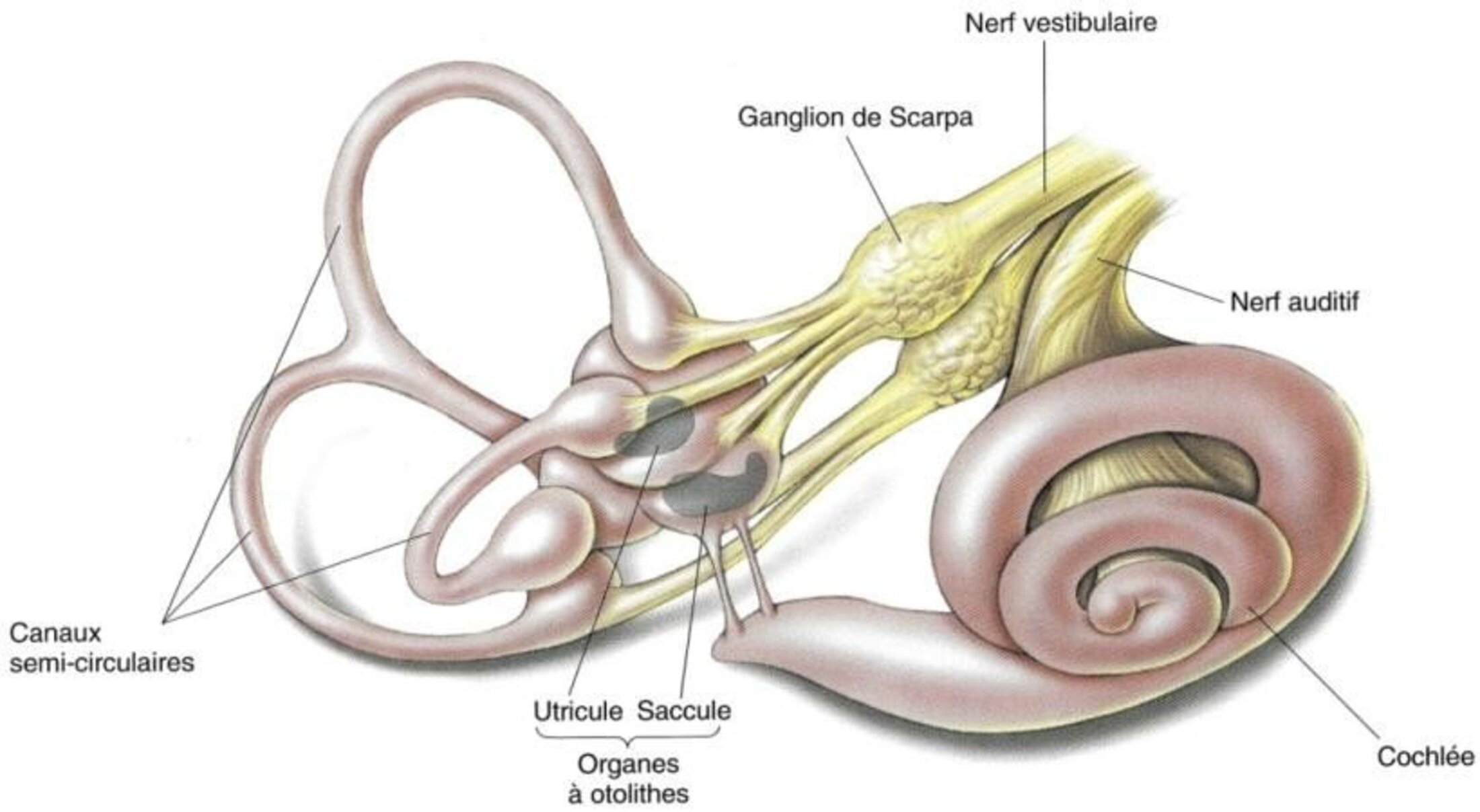
Pour faire simple, chaque cellule de la cochlée libère son glutamate quand elle reçoit la fréquence qui lui correspond. La forme logarithmique de la cochlée permet de rassembler des fréquences très éloignées (aigües et graves) en un lieu très restreint tout en conservant les différences et en distribuant chaque fréquence de son à la bonne cellule placée en un lieu précis du corridor hélicoïdal de la cochlée. Cette parfaite distribution en un lieu restreint, c’est l'effet de la transformation des produits en sommes, l’effet logarithme.
En résumé la magie du logarithme permet d’entendre une gamme de son très étendu, de fréquences et de volumes très différents. C’est l’effet logarithme qui nous permet d’entendre quelqu’un qui chuchote dans un bar. C’est l’effet logarithmique qui nous permet de reconnaitre les différents instruments qui jouent simultanément au sein de l’orchestre. Le réglage du volume sur votre téléphone est une échelle logarithmique transformée visuellement en une échelle linéaire avec un curseur qui se promène de gauche à droite. L’échelle linéaire visuelle vous permet de promener le curseur d’une même division à droite ou à gauche de l’échelle, mais les écarts auditifs sont dans une échelle logarithmique afin que la linéarité du mouvement de votre doigt corresponde à la « logarithmie » (néologisme) de votre ouïe.
Sans logarithme, nous n’entendrions que celui qui parle fort, nous n’entendrions pas les plus faibles…
Vous me voyez venir ? ... Oui, j’y suis.
Comment faire en sorte que les paroles multiples des citoyens, si faibles ou si fortes soient elles puissent être entendues en un lieu aussi restreint que le lieu du pouvoir ?
L'Assemblée Nationale, une grande cochlée.
J’ai un début d'essai de réflexion pour une tentative de proposition: cassons l’hémicycle de l’Assemblée Nationale. Cet amphithéâtre de régularité radiale et linéaire, où seuls les plus forts (les lobbys?) arrivent à se faire entendre, transformons le en grande oreille logarithmique, en grande cochlée. Pour que tous les bruits de natures différentes et tous les volumes soient perçus, identifiés, reconnus et visibles dans les débats, dans une organisation où tout apparaît à portée de la réflexion citoyenne et parlementaire. Chaque député ou groupe de députés peut être, c’est une image, une cellule de la cochlée. Reproduisons ce schéma dans les permanences de député. Cassons le bureau du député, le petit bureau austère ouvert un après-midi par semaine, organisons pour chaque député sa cochlée de circonscription avec des citoyens cellules, arrêtons de faire des pseudo-débats en disposant les citoyens en cercle autour d’un Président ou d’un.e Ministre, cercles au centre desquels ne peuvent sortir qu’un brouhaha ou, au pire, et c’est malheureusement le cas, des réponses toutes préparées, dirigées par l’exécutif toujours au centre et cautionnées par un simulacre d’approbation populaire.

Agrandissement : Illustration 6

Attention, ne faites pas l’erreur de penser que le centre linéaire et radial de l’hémicycle vers lequel converge le pouvoir, les Ministres et le Président, deviendrait le centre de la cochlée. Dans la cochlée la répartition le long de l’hélicoïde se fait en fonction d’une typologie adaptée au lieu de traitement. A l’entrée de la cochlée, les basses fréquences, les sons graves, au centre de la cochlée les hautes fréquences, les sons aigus. Les places des députés pourraient être réparties en fonction des textes de loi sur lesquels ils travaillent, des avancements dans les lectures ou des avancements en commission, en fonction de la criticité, etc... Et bien sûr dans cette approche, la place de chaque député n'est pas fixe, elle serait fonction des sessions, de la typologie des débats, du rôle qu'ils ont à jouer et de l’affluence.
Voilà pour un début de réflexion sur une des formes de nos institutions, mais j’irai plus loin avec un sujet qui me tient plus à cœur et me semble plus crucial.
Du logarithme dans les règles de l'économie
Aujourd’hui, nous manipulons l’économie essentiellement avec des échelles linéaires.
Une augmentation de salaire est un pourcentage, une croissance est un pourcentage, un bénéfice est un pourcentage, un déficit aussi, une taxe est un pourcentage, l’économie est sous l’égide du pourcentage. Les réglementations fixent des pourcentages. Le pourcentage, c’est la règle de trois, une règle d’or que l’on apprend très tôt à l’école (à ne pas confondre avec le nombre d’or qui est une construction logarithmique). Le pourcentage, c’est le linéaire, la multiplication, la division, le cercle dans lequel tout est à la même distance, l’hémicycle. Le pourcentage, on l’apprend sans même la connaître. On coupe un gâteau avec, on partage les bonbons comme on partage des bénéfices. On baigne dans le pourcentage et sa règle de trois.
Ne soyez donc pas surpris si nous l’utilisons pour appliquer une augmentation de salaires, une taxe ou un suffrage. C’est naturel pour le plus enfantin des adultes. Tout le monde comprend, personne n’y trouve à redire.
Sauf quand ça fait un peu trop, ou pas assez. Alors, on se dit qu’il faut faire de la justice, parce que les mathématiques ont des limites. Alors on fait des escaliers, on fait des suffrages indirects, des cartes électorales, on fait des tranches, en 3, en 4, en 16, comme dans l’impôt sur le revenu. On fait des escaliers à droite, à gauche, on fait des sous-escaliers qui montent qui descendent, toujours des escaliers droits, linéaires, et très vite ça devient des sujets qu’on ne peut comprendre que sur les bancs de l’ENA. Vous voyez c’est trop compliqué, le peuple ne saurait ni comprendre, ni faire. Chacun des énarques de s'en convaincre, par nature de l'émergence de cette pensée, la pensée unique de nos élites, la référence de leur action, de leur nature, de leur savoir-être, et une pensée qui les arrange finalement car elle justifie le principe de leur existence.
Les croissances et décroissances linéaires, les représentativités linéaires font de nos société des groupes distendus dont les extrêmes ne peuvent plus ni se voir , ni s’entendre, trop éloignés, comme pour notre métaphore des écoliers. Avec nos méthodes linéaires, aujourd’hui, un citoyen ne peut plus ni se faire voir ni se faire entendre d’un président, un ouvrier ne peut plus ni se faire voir ni se faire entendre d’un PDG, un pauvre ne peut plus ni se faire voir ni se faire entendre d’un riche, et la richesse, devenue sourde et aveugle, écrase le "reste" de leur masse incommensurable sans même s’en rendre compte... en s'effondrant sur elle-même.
La fonction inverse du logarithme est l’exponentielle. Nous parlons couramment des écarts de richesses qui grandissent de manière exponentielle. Si nous ne transformons pas le produit en somme, alors l’exponentielle s’en mêle par la multiplication entre elles d'échelles linéaires. Si vous appliquez tous les ans une même augmentation de salaires en pourcentage, l’augmentation se multiplie à celle de l’année précédente, et d’une croissance linéaire affichée, vous obtenez un croissance réelle sur la durée en forme d'exponentielle. C’est inévitable, c’est mathématique. Basique. Les banquiers le savent lorsqu’ils vous prêtent de l’argent, leurs tableaux d’amortissement avec un taux apparent linéaire, le taux du prêt, appliquent une formule qui embarque le taux d’intérêt dans une exponentielle, l’inverse du logarithme. Vous comprenez pourquoi ?
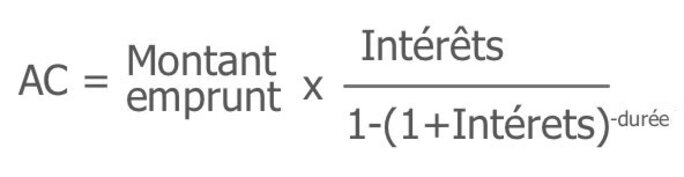
Voyez avec l’illustration ci-dessus de la formule qui permet de calculer un mensualité (AC) en fonction du montant emprunté, du taux d’intérêt fixe et de la durée (en tout petit à droite). La durée est introduite dans la formule par une puissance, c’est à dire une exponentielle. En conséquence, le coût total du prêt augmente exponentiellement avec la durée. Il n’augmente pas de manière linéaire, régulière, comme un taux fixe en pourcentage pourrait le laisser croire.
Alors mon interrogation est la suivante : est-ce que réviser notre algèbre économique sous l’angle du logarithme serait un changement d’échelle qui pourrait améliorer nos sociétés ?
Peut être.
Certainement.
Je vous accorde que ce n’est pas simple. Mais nous gagnerons à y réfléchir.
Intrinsèquement le logarithme est riche car il est ajustable, l’effet logarithmique peut être plus ou moins prononcé en fonction de la base logarithmique choisie et nous pouvons travailler avec des bases logarithmiques qui elles-mêmes progresseraient suivant une règle logarithmique, ce qui aurait pour effet d’additionner les effets (souvenez-vous le produit transformé en somme), comme l’oreille qui enchaîne l’effet de l’oreille externe et l’effet de l’oreille interne.
Ouvrez les yeux sur le monde. Toute est logarithmique. Sans le logarithme et son « anti » l’exponentielle, nous ne pourrions sonder ni l’infiniment petit, ni l’infiniment grand. La croissance organique est logarithmique. La croissance des plantes est logarithmique, elle se décline en diverses fractales qui nous subjuguent. Chez l’humain (chez l’animal aussi d’ailleurs), la croissance du nourrisson jusqu’à la taille adulte est une courbe logarithmique conséquence du mécanisme de la division cellulaire : la multiplication qui devient somme. Si à l’âge adulte nous croissions au rythme du nourrisson, nous serions d’énormes êtres informes et croulerions sous notre propre masse, comme dévorés par un cancer que nous ne comprendrions pas. Le logarithme est un processus mathématique qui permet aux organismes en croissance de se tenir et de se contenir tout en conservant leur intégrité et leurs propriétés. L’arbre est une forme logarithmique. L’architecte Le Corbusier a créé un paradigme architectural avec le nombre d’or, construction logarithmique, nombre ancestral que certains attribuent à Khéops, nombre qui nous compose, car, je l’ai expliqué, le vivant est une construction logarithmique. L’application pratique du nombre d’or en architecture, c’est la dimension des portes et des fenêtres, la dimension des pièces dans un logement, la dimension des meubles… Le Corbusier n’a pas réellement inventé, il a surtout montré ce que nous sommes, comment nous bougeons…
Pour un enfant qui fait la moitié de la taille adulte, le monde ne lui paraît pas deux fois plus grand, mais huit fois plus grand (23 = 2 x 2 x 2 = 8, un produit pour chaque dimension spatiale). Oui, je sais, c’est dur à comprendre, ou plutôt, à ressentir. Mais c'est bien un effet exponentiel (de puissance) qui est inversement la conséquence du rythme logarithmique de notre croissance.
Intuitivement, si nos échelles d’évolutions étaient logarithmiques, nos sociétés seraient moins distendues tout en proposant une graduation et du discernement, à l’instar des instruments dans un orchestre.
Les plus riches opposeront qu’ils deviendraient moins riches… Oui ils deviendraient moins riches en valeurs absolues, mais ils y gagneraient en stabilité, car si le logarithme permet de raisonner la croissance en contenant les mouvements, il permet tout autant de raisonner la décroissance. N'est-ce pas ce dont nous avons besoin aujourd'hui pour arrêter de faire bouillir la planète ?
Alors mesdames et messieurs économistes, poètes, physiciennes, agriculteurs, médecins, avocates, ministres, ouvrières, institutrices, managers, directrices, infirmiers, député.e.s, président.e [...], chômeuses, chômeurs, SDF, qu’en dites vous ? On révise ?
À vos avis.
Mais surtout, … surtout, ne me dites pas que ce n’est pas possible. Au prétexte que personne au monde ne fait ça, que, en Allemagne ou en Italie, ils ne font pas comme ça. Nous n’en pouvons plus d’entendre qu’il faut faire comme à l’étranger, qu'il faut copier, qu’il faut avoir le même taux de chômage qu’à l’étranger, le même nombre de fonctionnaires, la même croissance, la même dette. Quand j’entends cet argument, j’entends des politiques en mal d’intelligence ou de créativité, j’entends des politiques démissionnaires, j’entends des politiques sourds et aveugles. Et ça me met très en colère.



