Agrandissement : Illustration 1
Le public de la revue est surtout composé de militants politiques et syndicaux. En quoi la conjecture de Kakeya peut-elle donc intéresser des ouvriers, des paysans, des agents EDF, des infirmiers, des conseillers municipaux de banlieue, des profs de lettres ?
Un président de la République s’était posé une question similaire au sujet de La princesse de Clèves… Pourquoi la culture s’adresserait-elle aux seuls intellectuels ? Car c’est bien de culture dont il s’agit ici, de culture scientifique précisément. Notre livre présente en particulier une invention fondamentale âgée de plus de trois siècles et qui est pourtant encore largement méconnue. Voltaire l’appelait « vérité sublime », elle est restée dans l’histoire sous le nom plus ingrat de « calcul différentiel ». Ce calcul, inventé par Newton et Leibniz, a transformé les sciences en profondeur en les dotant d’un outil d’une puissance considérable pour modéliser le monde. Aujourd’hui, on le retrouve dans d’innombrables domaines, depuis la physique théorique jusqu’aux sciences du vivant. Il est également massivement employé en économie, par exemple dans l’optimisation des rendements ou des investissements. Compte tenu de son importance, il est singulier qu’il soit si peu expliqué. Nous avons voulu remédier à cette insuffisance en exposant le calcul différentiel au travers d’une question de mathématique compréhensible par tous : la conjecture de Kakeya.
Peux-tu nous expliquer en peu de mots et avec des dessins de quoi il s’agit ?
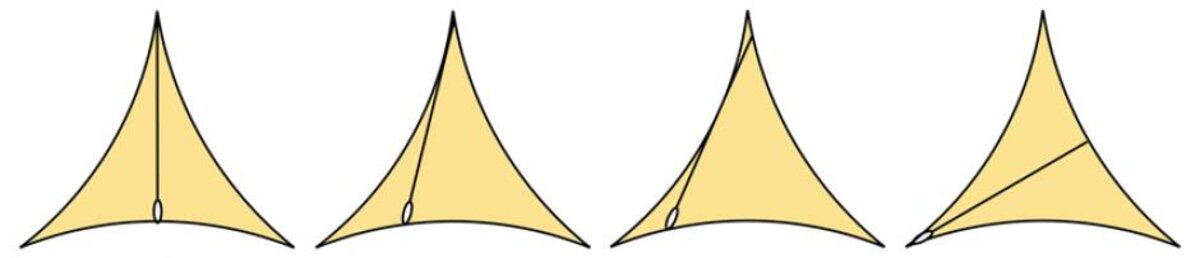
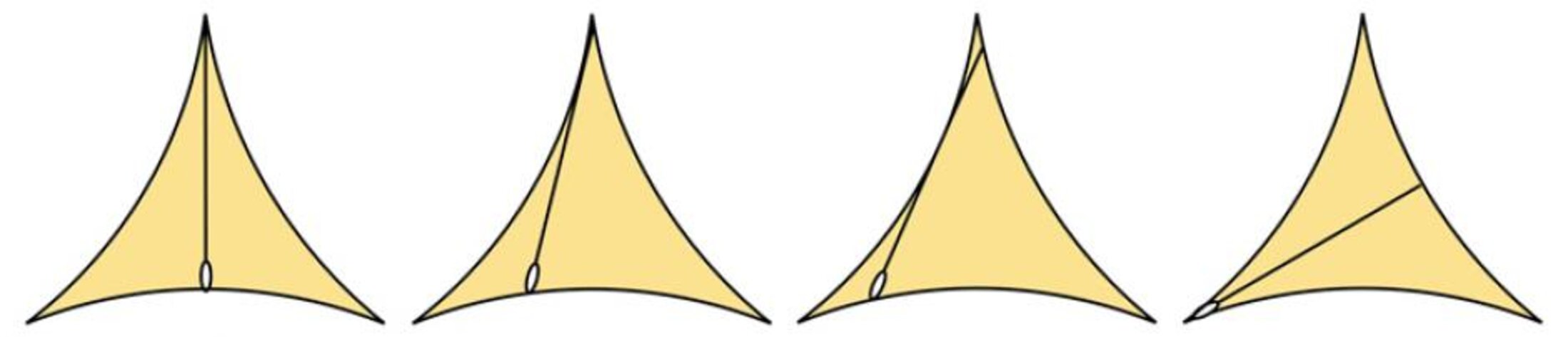
Au départ, il s’agit d’un problème géométrique relativement insignifiant et même un peu crispant… Mais, qui va se révéler être un véritable joyau, capable de nous éclairer sur des pans entiers des mathématiques. Voici la question initiale telle que l’a formulée Soïchi Kakeya en 1917 : quelle est la plus petite surface à l’intérieur de laquelle il est possible de déplacer une aiguille de manière à la retourner complètement ? La réponse évidente c’est de faire tourner l’aiguille sur elle-même. La surface balayée est un disque dont l’aiguille est un diamètre. Pourtant, on peut faire mieux. Les dessins ci-dessous (fig. 1) montrent comment l’aiguille peut se retourner dans une figure qui ressemble à un triangle aux bords concaves et dont la surface est deux fois plus petite.
Il ne s’agit là que d’un exemple. Il n’est pas optimal. Il ne donne pas la réponse à la question de Kakeya. C’est là une des difficultés du problème. Chaque fois que l’on trouve une nouvelle façon de retourner l’aiguille, il reste toujours possible qu’une découverte ultérieure vienne réduire encore la surface nécessaire. Comment dans ces conditions être assuré d’avoir la solution définitive ? La manière dont cette question se résout constitue l’un de ces coups de théâtre ahurissants qui émaillent l’histoire des sciences. Mais je n’en dirai pas plus ici de peur de gâcher le plaisir de la lecture de l’ouvrage.
Et cette « conjecture » de Kakeya, est-elle résolue ?
Oui… et non ! C’est là, précisément, que notre « question de Kakeya » qui jusque-là n’avait pas grand intérêt va prendre toute son ampleur. La question de Kakeya a été résolue en 1928 mais au cours de cette résolution les mathématiciens ont été conduits à considérer une version plus générale du problème initial : la « conjecture de Kakeya ». Ici, on abandonne le mouvement, qui figurait dans la « question », pour ne chercher plus que les figures qui contiennent l’aiguille dans toutes les directions de notre espace à trois dimensions, voire d’espaces de dimensions plus grandes. De telles figures sont si complexes qu’il est impossible de les imaginer. Sont-elles diaphanes ? opaques ? squelettiques ou consistantes ? Personne ne le sait. La conjecture de Kakeya proclame qu’elles ne peuvent être trop fines, qu’elles ont toujours une certaine épaisseur. Cette conjecture n’est pas résolue, et ce en dépit des efforts acharnés d’un nombre conséquent de mathématiciens dont plusieurs ont obtenu la médaille Fields (équivalent du prix Nobel pour les mathématiques). Les raisons d’un tel acharnement ? Une succession de rebondissements spectaculaires qui ont révélé des liens insoupçonnés entre la conjecture de Kakeya et d’autres domaines des mathématiques dont en particulier la théorie des nombres. Car oui, il existe une connexion souterraine entre le retournement d’une aiguille et la question reine des mathématiques, celle de la répartition des nombres premiers ! Ces connexions sont extrêmement prisées par les mathématiciens car elles leur offrent de nouveaux angles de vue, de nouvelles perspectives. Soudain, une vérité lumineuse remplace une certitude calcifiée, une question insoluble trouve sa réponse limpide et manifeste. La découverte ne consiste pas à chercher de nouveaux paysages mais à avoir de nouveaux yeux, écrivait Proust. Les mathématiciens espèrent de nouveaux yeux avec la conjecture de Kakeya.
Ce livre n’est-il pas un peu dans la lignée des Éléments de géométrie (1741) et d’algèbre (1746) de Clairaut, à savoir introduire les notions fondamentales de mathématiques, au fur et à mesure, quand on en a besoin pour résoudre un problème et non, comme usuellement, de façon formelle, magistrale et a priori ?
Nietzsche donne à Ainsi parlait Zarathoustra le sous-titre suivant « Un livre pour tous et pour personne ». Cette formule sonne comme une mise en garde. Quand on a pour objectif de rendre le calcul différentiel accessible à tous, comment éviter que le livre ne soit finalement compris par personne ? Nous avons effectivement suivi les pas de Clairaut. Le calcul différentiel est introduit progressivement tout au long de l’ouvrage pour servir le récit principal qui est celui du problème de Kakeya. Le texte est agrémenté d’un très grand nombre de figures. Il prend le temps de poser le contexte, de conter les anecdotes, de décortiquer les difficultés, d’exposer les idées cardinales, d’en montrer leur force et d’ouvrir sur les perspectives qu’elles engendrent. Chemin faisant, le lecteur est invité à explorer le vaste domaine des mathématiques actuelles et à découvrir nombre d’objets stupéfiants : surfaces sans aire, fractales, quatrième dimension, systèmes chaotiques, etc. Bref, le problème de Kakeya joue le rôle d’un fil d’Ariane qui conduit le lecteur depuis le calcul différentiel jusqu’au cœur des mathématiques. Aussi bien dans le fond que dans la forme, nous sommes donc très loin d’une présentation magistrale. Et comme on s’en doute, la rédaction du livre fut tout sauf directe et facile : elle s’est étalée sur plus d’une décennie. Il faut ici remercier l’Institut Camille Jordan (Lyon - Saint-Étienne) et le « Labex Milyon » pour leur soutien et leur confiance durant ces longues années.
Publier un livre imprimé tout en le mettant en accès libre sur le net n’est-ce pas suicidaire pour un éditeur ?
Je viens de recevoir un courriel de l’éditeur m’informant qu’une troisième impression de l’ouvrage allait être nécessaire. L’accès libre n’a donc pas tué la vente, loin de là. Au départ, Jean-Luc Rullière et moi ne désirions pas spécialement éditer l’ouvrage au sens classique. En octobre 2011, nous avons décidé de mettre le fichier PDF de l’ouvrage en accès libre sur Internet. Il a été téléchargé presque 6 500 fois et nous avons reçu de nombreuses lettres nous demandant si une version papier était disponible. Nous nous sommes alors mis à la recherche d’un éditeur acceptant de publier le livre tout en laissant l’accès gratuit au fichier PDF. ENS-Éditions a répondu favorablement, nous les remercions grandement. Nous avons bien entendu renoncé à nos droits d’auteur. Comme dit le proverbe indien : « tout ce qui n’est pas donné est perdu ».
*Vincent Borrelli est mathématicien. Il est maître de conférences à l’université Lyon-1.
Propos recueillis par Pierre Crépel.
La Revue du Projet n° 56, avril 2016



