Il est utile de comprendre quelques notions de statistiques pour éviter d’interpréter de travers les études scientifiques menées sur des traitements.
Ce qui suit ne cherche pas à entrer dans des considérations médicales, mais à rendre accessible le sens de quelques notions telles que « statistiquement significatif » ou « p-value », dont il est souvent question à propos des études scientifiques, et qui donnent parfois lieu à des interprétations hasardeuses.
On cherchera notamment à montrer pourquoi une étude (sur un traitement, par exemple) dont le résultat est statistiquement non significatif ne permet pas forcément de conclure que le traitement est inefficace. Et comment elle peut contribuer à construire un savoir scientifique.
Les jeux de hasards et la science
Pour faciliter la compréhension, on raisonnera sur des exemples simples : sans s’arrêter à des considérations morales, on partira de l’exemple de dés pipés.
Un dé est un petit cube, dont chaque face est marqué d’un chiffre, de « 1 » à « 6 ». Il est très utilisé dans les jeux de société et de hasards et un dé normal a exactement autant de chances de tomber sur n’importe laquelle de ses 6 faces.
Mais une façon de tricher au jeu est d’utiliser un dé pipé, c’est à dire un dé qui tombe plus souvent sur une certaine face (par exemple sur le « 6 ») qu’un dé normal. Un dé normal doit avoir une chance sur 6 de tomber sur le « 1 », une chance sur 6 de tomber sur le « 2 » etc. Un dé qui a une chance sur 5,9 de tomber sur le « 6 » est un dé pipé. Un dé qui a une chance sur 3 de tomber sur le « 6 » est très pipé.
Mais comment savoir si un dé est pipé ? Certes on peut utiliser du matériel technique permettant de mesurer la répartition de densité de matière dans le dé, par exemple, mais il existe un moyen accessible à tout le monde sans matériel : les statistiques.
Les statistiques sont un domaine des mathématiques, qui permet de calculer ce genre de choses. Grâce aux statistiques, si on jette un dé suffisamment de fois, on peut savoir, en faisant quelques calculs, s’il est pipé ou non.
Le principe est le suivant : si un dé n’est pas pipé, on sait que le « 6 », comme n’importe quelle face, a une chance sur 6 de tomber à chaque lancer. Les statistiques permettent de calculer exactement la probabilité de tomber plus d’un certain nombre de fois sur le « 6 » si on lance le dé un nombre donné de fois. Avec un dé qu’on ne connaît pas, et qu’on veut tester, on le lance plusieurs fois, on note le résultat (c’est-à-dire le nombre de fois où le « 6 » est sorti), et on regarde si ce résultat était probable ou improbable avec un dé normal. Si on arrive à un résultat qui aurait été « étonnant » (improbable) avec un dé normal, on peut soupçonner le dé d’être pipé.
La puissance statistique des dés
Une question importante est « combien de fois faut-il lancer le dé pour savoir s’il est pipé ? ». Est-ce qu’il suffit de lancer le dé 3 fois ? Cent fois ? Un million de fois ?..
Le nombre de lancers nécessaires dépend de plusieurs choses : par exemple, plus le dé est pipé, moins il y a besoin de lancer le dé pour le savoir ; mais cela dépend aussi du degré de certitude que l’on veut acquérir. Parce qu’en réalité, si on ne s’appuie que sur les statistiques, on ne peut jamais être sûr à 100 % qu’un dé est pipé. Les statistiques permettent de dire « on est sûr à 90 % que le dé est pipé » ou « on est sûr à 97 % que le dé est pipé » ou « on est sûr à 99,9995 % que le dé est pipé », etc. Ou encore : « pour l’instant on ne peut pas savoir si le dé est pipé. »
Si, après avoir lancé un dé un certain nombre de fois, on a calculé, grâce aux statistiques, qu’on est sûr à 90 % que le dé est pipé, ça veut dire en gros qu’on a 9 chances sur 10 d’avoir raison si on dit que le dé est pipé. Et ça veut donc dire qu’il y a quand même une chance sur 10 qu’on se trompe. Autrement dit, si on est sûr à 90 % que le dé est pipé, cela signifie qu’il y a une chance sur 10 que le nombre un peu louche de « 6 » qu’on a obtenus en lançant le dé un certain nombre de fois, ait pu être obtenu avec un dé normal, pas pipé du tout.
La p-value, c’est statistiquement significatif ?
On peut donc poser la question de la certitude sous une autre forme : quelle est la probabilité qu’avec un dé parfaitement normal j’obtienne le résultat que j’ai trouvé en lançant le dé que je cherche à tester. Cette probabilité qu’un dé normal obtienne un résultat aussi louche que celui que j’ai obtenu, c’est exactement la probabilité que je me tromper si je dis que mon dé est pipé, et c’est ce qu’en statistiques on appelle la « p-value1 ». Cela peut se calculer précisément, ce qu’on ne fera pas ici. Mais on peut au moins expliquer ceci : la p-value est un nombre compris entre 0 et 1, qui mesure nos chances de nous tromper si on affirme que le résultat observé n’est pas dû au hasard. Une p-value de 0,1 (ce qui est noté « p=0,1 ») signifie qu’on aurait eu 10 chance sur 100 d’arriver au même résultat avec un dé normal. Une p-value de 0,05 signifie qu’on avait 5 chances sur 100 d’arriver au même résultat avec un dé normal. Une p-value inférieure à 0,001 (« p<,001 ») signifie qu’un dé normal avait moins d’une chance sur 1000 d’arriver au même résultat.
Plus la p-value est proche de zéro, plus le résultat auquel elle est associée est statistiquement significatif.
Les statistiques permettent donc, grâce à des calculs, de répondre aux deux questions suivantes, qui sont en fait la même question : « en jetant mon dé un certain nombre de fois, j’ai obtenu un certain résultat ; quelle est la probabilité que ce résultat ait pu être obtenu avec un dé normal ? Et donc à quel point je peux être sûr que le dé est pipé ? »
Une dose d’arbitraire dans la science
Mais puisqu’on ne peut jamais être sûr à 100 %, à partir de quel degré de certitude s’autorise-t-on à penser que le dé est pipé ?
Eh bien dans de nombreux domaines, et notamment en recherche pharmaceutique, par convention, on considère que 95 % de certitude, c’est suffisant pour affirmer quelque chose. Ce seuil de 95 % est vraiment une convention, avec sa part d’arbitraire, mais il est généralement adopté. Ce n’est pas le cas partout : dans des secteurs tels que l’aéronautique, on a besoin de degrés de certitude bien plus élevés, par exemple pour évaluer le risque qu’une pièce mécanique se casse : on ne se contente pas d’être sûr à 95 %...
Mais pour nos dés, on adoptera la convention retenue pour les études sur des médicaments : si le résultat de nos lancers de dés nous donne un degré de certitude en-dessous de 95 %, c’est-à-dire si la p-value est supérieure à 0,05, on dira que le résultat de ces lancers de dés n’est pas statistiquement significatif. Si la p-value est plus petite que 0,05, on dira que le résultat est statistiquement significatif, et on affirmera qu’on a prouvé que le dé est pipé.
On ne fera pas de calculs ici, mais on donnera des exemples un peu extrêmes, pour montrer qu’on peut facilement comprendre certains enjeux des essais cliniques.
Pour illustrer de façon perceptible ce qui précède, on peut imaginer qu’on lance notre dé 2 fois. Si on tombe deux fois sur le « 6 », on peut avoir un mini-mini soupçon, mais on sait bien que ça peut très bien arriver avec un dé normal (pas pipé), et les statistiques nous le confirmeront : avec deux lancers de dé, on ne peut pas du tout être sûr que le dé est pipé, même s’il tombe les deux fois sur le « 6 ».
On notera d’ailleurs que même avec un dé tellement pipé qu’il tombe une fois sur deux sur le « 6 », il est parfaitement possible que si on le lance deux fois, on tombe sur le « 3 » et sur le « 5 », par exemple. On n’aurait alors aucun indice que le dé est pipé et rien ne nous autoriserait à penser qu’il l’est. Donc avec deux lancers, on ne peut être sûr de rien : ni que le dé est pipé, ni que le dé n’est pas pipé.
Relance les dés, Dédé !
Maintenant, imaginons qu’on lance notre dé 1 million de fois, et qu’on tombe 181795 fois sur le « 6 », c’est-à-dire environ une fois sur 5,5. Bien que l’écart entre une fois sur 6 (c’est-à-dire 166667 fois sur un million) et 1 fois sur 5,5 (nos 181795 fois sur un million) ne soit pas spectaculaire, les statistiques nous disent qu’avec un dé normal, il est extrêmement improbable (même si en théorie ce n’est pas impossible) qu’une série d’un million de lancers atteigne les 181795 « 6 ». C’est tellement improbable qu’on n’a quasiment aucune chance de se tromper en disant que le dé est pipé.
Autre exemple : si on lance un dé 24 fois de suite, et que sur les 24 fois, on tombe 21 fois sur le « 6 », on aurait de forts soupçons que le dé est pipé, et même extrêmement pipé. Et les statistiques nous le confirmeront : on a infiniment peu de chances de se tromper si on affirme que ce dé est pipé. Dans ce cas, il n’est pas besoin de le lancer un million de fois. Mais cela ne pourrait arriver que dans le cas d’un dé pipé à l’extrême.
Mais si en lançant le dé 24 fois on tombe 7 fois sur le « 6 » (et environ 3 ou 4 fois sur chacun des autres numéros), eh bien les certitudes sont minces. Sept fois, c’est plus que 4 fois (qui correspondrait à 1 fois sur 6 après 24 lancers), mais cela reste un score plausible avec un dé normal. Si le dé est pipé, il l’est beaucoup moins fortement que dans le cas précédent (21 « 6 » sur 24 lancers) et il faudra un plus grand nombre de lancers pour le savoir.
Traitons le dé
Ces quelques notions étant un peu débroussaillées, imaginons cette expérience : on prend un dé a priori normal, acheté dans le commerce, et on lui applique un « traitement » : on creuse un peu le dé ici, on injecte un peu de matière là, on applique un vernis sur certaines faces et un vernis différent sur d’autres faces etc., dans le but de piper le dé, afin qu’il tombe plus souvent sur le « 6 » que sur les autres faces.
Comment savoir avec 95 % de certitude si le traitement du dé a marché, c’est à dire s’il fait sortir le « 6 » plus souvent qu’une fois sur 6 ?
Eh bien il faut lancer le dé un certain nombre de fois. On ne sait pas trop à l’avance combien de fois : ça dépend de l’efficacité du traitement ; si le dé est très pipé grâce au traitement, il suffira d’un plus petit nombre de lancers que si le traitement a seulement légèrement pipé le dé. (Et si le traitement n’a pas marché, il faudra décider d’arrêter de lancer le dé, par exemple quand on aura calculé que, vu le nombre de lancers déjà effectués, même si le dé est pipé, il l’est tellement peu que cela n’a pas d’intérêt.)
Imaginons donc qu’on a appliqué notre traitement au dé et qu’on le lance 100 fois. Un dé normal devrait donner en moyenne 16 ou 17 fois le « 6 ». Imaginons qu’avec notre dé traité, le « 6 » sorte 21 fois. Les statistiques permettent de calculer la p-value p=0,15. Cela veut dire que ce n’est pas un résultat invraisemblable pour un dé normal. Ca ne permet donc pas de prouver (c’est-à-dire de savoir avec plus de 95 % de certitude) que le dé est pipé. Autrement dit, le résultat n’est pas statistiquement significatif.
Il faut donc encore lancer le dé.
Mais imaginons qu’on n’ait pas le temps de s’en occuper, et qu’on demande à d’autres personnes de lancer le dé, chacune 100 fois, et de compter les « 6 » obtenus.
Imaginons qu’une dizaine de personnes s’attellent chacune leur tour à ce travail : chacune des dix lance notre dé 100 fois et nous envoie son résultat : deux d’entre elles sont tombées 21 fois sur le « 6 », une autre 18 fois, deux autres 23 fois, une autre 16 fois, deux autres ont lancé le dé 50 fois seulement et sont tombées sur le « 6 » 11 fois pour l’une et 12 fois pour l’autre etc. Au total, sur 1000 lancers, le « 6 » est sorti 210 fois.
Ce que disent les statistiques, c’est que ce résultat de 210 « 6 » obtenus sur 1000 lancers est, lui, statistiquement significatif, et que le dé est en fait très pipé : un dé non-pipé ou seulement un peu pipé aurait moins de 5 % de chances de permettre que le « 6 » sorte autant de fois. Ici, le dé est suffisamment pipé pour que le « 6 » sorte au moins une fois sur 5. Le traitement a très bien marché.
Dans cette expérience, chacune des personnes qui a lancé 100 fois le dé est tombée sur un résultat statistiquement non-significatif (dont on a calculé que la p-value était supérieure à 0,05), qui ne permettait donc pas de savoir si le traitement avait suffi à piper le dé. Mais leurs résultats, mis ensemble, permettent d’atteindre une « puissance statistique » suffisante pour affirmer (avec moins de 5 % de chances de se tromper, c’est-à-dire avec une p-value p<0,05) que le dé est pipé, c’est-à-dire que le traitement a été efficace.
Essais transformés et méta-analyse
Avec cet exemple, on a montré qu’il fallait se méfier de plusieurs raccourcis. Contrairement à des croyances largement répandues :
- un essai dont le résultat n’est pas statistiquement significatif ne signifie pas que le traitement testé ne marche pas. Dans certaines conditions, un traitement très efficace peut donner lieu à des résultats statistiquement non significatifs.
- un essai dont le résultat n’est pas statistiquement significatif n’est pas inutile. Il peut éventuellement être rassemblé avec d’autres résultats pour obtenir une puissance statistique suffisante pour acquérir une certitude.
- « il n’est pas prouvé que ça marche » n’a pas du tout le même sens que « il est prouvé que ça ne marche pas ».
Bien sûr, l’essai d’un traitement sur des humains n’est pas aussi simple qu’un lancer de dé. Mais le principe statistique est le même : la puissance statistique d’un essai dépend à la fois de l’efficacité du traitement testé, du nombre de personnes incluses dans l’essai, mais aussi de ce que l’on a choisi de mesurer, par exemple.
Pour évaluer un traitement, il est possible de rassembler plusieurs essais pour tenter d’obtenir une certitude grâce à leur puissance statistique cumulée. Cela suppose que de nombreuses conditions soient réunies : notamment, la qualité des essais doit être suffisante, les risque de biais doivent être maîtrisés, il faut pouvoir évaluer les facteurs de confusion etc. C’est un travail que savent mener des scientifiques spécialisés, et c’est ce qu’on appelle des méta-analyses.
Dans le cas de certains traitements envisagés contre le Covid-19, on est dans une situation de ce type : plusieurs petits essais, menés dans différents pays avec peu de financements, ont obtenu des résultats statistiquement non significatifs. Mais des méta-analyses ont été menées grâce à ces essais, et ont conclu à une sérieuse présomption d’efficacité. C’est le cas notamment pour l’ivermectine, avec les méta-analyses de Lawrie et al., de Nardelli et al. et plus récemment celle de Bryant et al., menée selon la rigoureuse méthodologie Cochrane.
Et le groupe contrôle ?
On l'aura sans doute remarqué : pour tester le dé traité, on ne s'est pas servi d'un "groupe contrôle", et la question mérite d'être soulevée. On a en effet commencé notre expérience de traitement du dé en ayant la certitude qu'avant le traitement c'était un dé normal. Or, on connaît suffisamment bien le comportement des dé normaux pour ne pas avoir à comparer notre dé traité à un dé non traité. On sait calculer, grâce aux statistiques, quelles chances un dé normal a de tomber sur le « 6 » si on le lance un certain nombre de fois ; il ne sert à rien de prendre un dé normal pour faire les essais et le lancer 100 fois ou 1000 fois en parallèle du dé traité.
Mais par exemple, si on n'était pas sûr de la qualité de notre dé avant le traitement... Comment savoir, après nos 1000 lancers, si c'est le traitement appliqué au dé qui l'a pipé, ou si le dé était déjà pipé avant le traitement ? Eh bien on ne peut pas savoir ! Pour en être sûr, il faudrait prendre un "dé contrôle", de la même marque que le dé qu'on a traité, et de le lancer aussi quelques centaines de fois pour savoir si lui aussi est pipé.
Oui, mais ça ne suffit pas : qu'est-ce qui nous prouve que l'usine de dés les fait tous identiques ? Imaginons qu'on n'en sache rien. Cette usine produit peut-être des dés pipés où le « 6 » sort plus souvent qu'une fois sur 6, d'autres qui sortent le « 6 » moins souvent qu'une fois sur 6, d'autres qui sont parfaitement équilibrés, etc. Dans ce cas, si les dés sont des individus différents les uns des autres, avec chacun sa personnalité, ses qualités et ses défauts, ses déséquilibres etc., il n'y a plus qu'une façon de procéder : traiter tout un groupe de dés, en espérant qu'il soit assez nombreux pour regrouper un peu toutes les personnalités de dés ; et prendre un autre groupe de dés, en espérant aussi qu'il soit représentatifs des variations de dés possibles, et se lancer dans des lancers... Ce qu'on comparera, c'est le comportement moyen du groupe traité avec le comportement moyen du groupe non traité. Et si on observe des résultats moyens différents pour les deux groupes, les statistiques nous permettront de savoir si cette différence est statistiquement significative ou pas, c'est-à-dire si on peut savoir avec moins de 5% de chances de se tromper que c'est le traitement qui a généré cette différence, ou si on peut soupçonner le hasard.
Remarquons qu'on s'approche de ce qui se passe pour les humains : les humains sont tous différents, et il est nécessaire de comparer des groupes, dont on fait en sorte qu'ils recoupent les mêmes variations humaines, pour savoir si un traitement est efficace ou non. Cela dit, on peut imaginer des cas où le comportement humain moyen est connu de façon suffisamment précise pour que ce que l'on sait déjà sur ce comportement suffise à comparer avec un groupe traité. Voici un exemple : imaginons qu'un chercheur mette au point une pilule qui rend les poumons capables de récupérer l'oxygène de l'eau de mer et qui permet de respirer en plongée pendant une heure. Imaginons qu'on fasse l'essai de cette pilule sur 3 personnes volontaires, et que toutes les 3 ressortent la tête de l'eau après une heure, ravies de leur expérience, disant que le premier moment où l'eau pénètre dans les poumons est un moment désagréable, mais qu'une fois ce cap passé, c'est confortable... Aura-t-on besoin de plonger sous l'eau un groupe contrôle pendant une heure pour s'assurer qu'il y a bien une différence ? Voilà qui soulèverait des questions d'utilité et d'éthique... Cet exemple extrême et irréaliste peut toutefois avoir de lointaines similitudes dans la vie réelle...
1La p-value n’est pas la seule façon proposée par les statistiques pour estimer la probabilité que le résultat obtenu soit simplement dû au hasard. Mais on n’abordera pas ici les autres notions, telles que l’intervalle de confiance.
Illustration pratique
Lecture d'une étude de Hashim et al., qui présente les résultats d'un petit essai contrôlé randomisé, mené en Irak sur 140 patients. Selon le paramètre étudié, les résultats sont statistiquement significatifs (p<0.05) ou non (p>0.05).
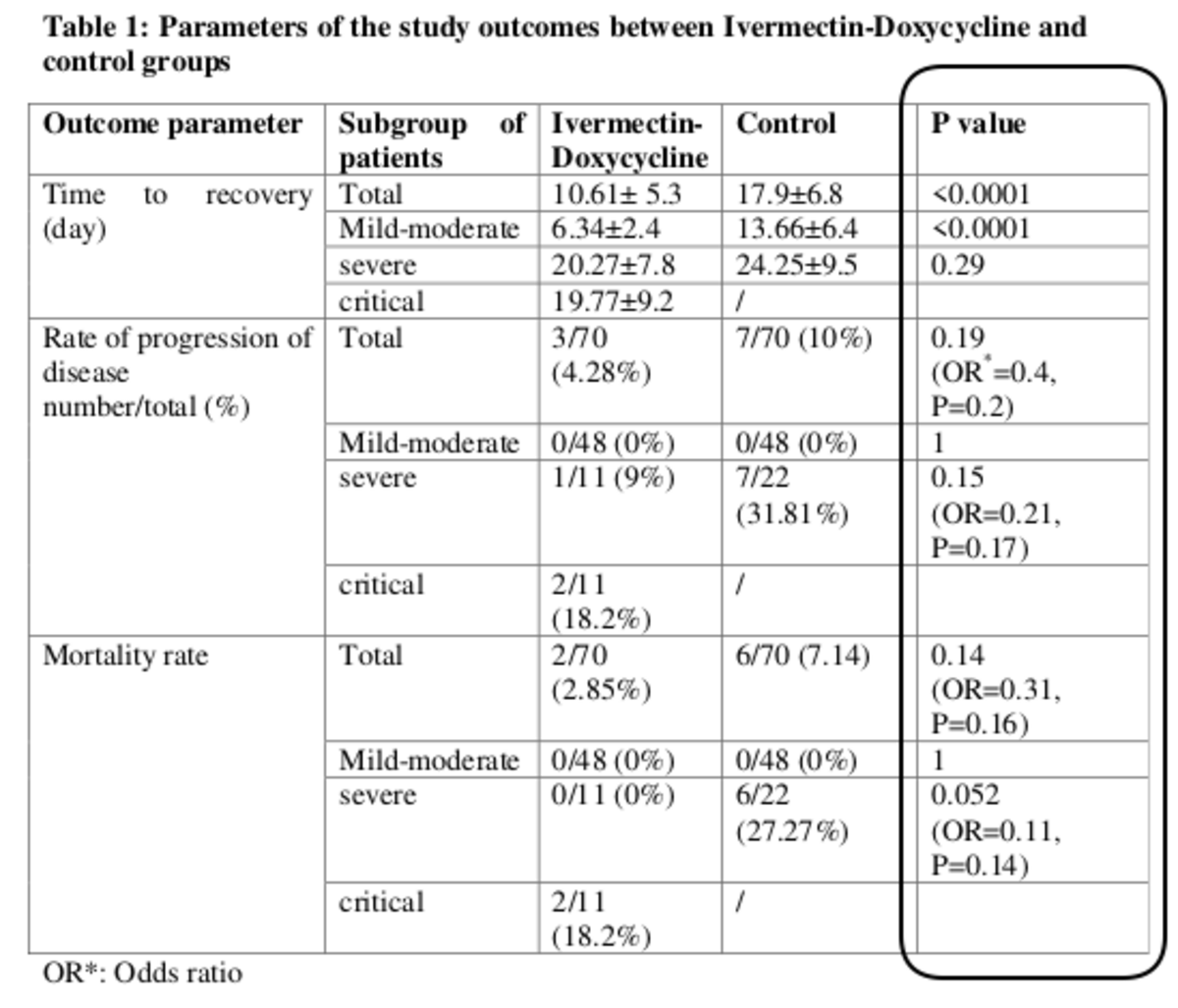
Regardons en détail cette étude et le tableau des résultats, reproduit ci-dessus. Quelques remarques seront formulées plus bas sur la fiabilité de cette étude, mais pour illustrer l'interprétation de la p-value et la question de la significativité statistique, on se placera dans l'hypothèse où l'étude est bien menée.
L'équipe de chercheurs testait un traitement : une bithérapie, composée d'ivermectine (200µg/kg pendant 2 à 3 jours) et de doxycycline pendant 5 à 10 jours.
Deux groupe de 70 patients étaient constitués de façon comparable : dans chaque groupe il y avait 48 patients atteints d'une forme légère ou modérée de Covid-19, et 22 patients atteints de formes plus graves ; dans le groupe traité il y avait 11 patients sévères et 11 patients dans un état "critique", mais le groupe contrôle ne comportait que 22 patients "sévères" et aucun dans un état critique.
Tous les patients, dans le groupe contrôle comme dans le groupe traité, recevaient le traitement standard ("standard of care"), pouvant s'adapter à leur état. La mise sous oxygène, par exemple, faisait partie du traitement standard, mais n'était administrée qu'aux patients en ayant besoin. La différence entre les patients était donc le traitement par bithérapie, que seul recevait le groupe traité.
Si on regarde en détail chaque ligne, on peut examiner le sens de la p-value indiquée dans la dernière colonne :
1ère ligne ("Time to recovery (day) / Total") : pour l'ensemble de chaque groupe (quel que soit l'état d'entrée du patient), le temps de rémission a été plus court pour les patients traités que pour les patients non traités. En moyenne, les patients qui ont guéri se sont remis en 10,61 jours s'ils étaient traités, et en 17,9 jours s'ils n'étaient pas traités ; et la différence observée sur les temps de guérison individuels est statistiquement significative puisque "p<0.0001". On a moins d'une chance sur 10.000 de se tromper si on dit que le traitement a en moyenne accéléré la guérison du groupe traité.
2ème ligne ("Time to recovery (day) / Mild-moderate") : pour les patients atteints de formes légères ou modérées de Covid (48 dans chaque groupe), le temps de guérison a été plus court dans le groupe traité que dans le groupe contrôle, de façon statistiquement significative : là aussi, p<0.0001, et on peut affirmer avec peu de risque d'erreur que le traitement a accéléré la guérison des patients qui présentaient un Covid-19 léger ou modéré.
3ème ligne : parmi les patients qui étaient dans un état sévère (11 dans le groupe traité et 22 dans le groupe contrôle) ceux qui ont guéri s'en sont sortis en moyenne plus vite s'ils étaient traités (20,27 jours) que s'ils ne l'étaient pas (24,25 jours). Mais puisqu'on lit "p=0.29", ce résultat-là n'est pas statistiquement significatif, et on ne peut pas exclure que ce soit le hasard et non le traitement qui a rendu la guérison plus courte chez les patients traités. On en peut pas l'exclure, et ce résultat ne prouve donc pas que le traitement a accéléré la guérison des patients en état sévère ; mais il ne prouve pas non plus que le traitement n'a pas eu d'effet ! Il donne un indice, en laissant un doute.
La 4ème ligne ("Time to recovery (day) / critical") ne comporte pas de p-value. Aucun patient du groupe contrôle n'étant en état critique, il n'a pas été possible de comparer les deux groupes.
Les 4 lignes suivantes concernent un autre critère : les auteurs comptaient dans chaque groupe le nombre de patients dont l'état s'aggravait.
5ème ligne : Pour l'ensemble des 70 patients du groupe traité, 3 se sont aggravés ; parmi les 70 du groupe non traité, il y en a eu 7. Il y en a donc eu davantage dans le groupe non traité, mais les statistiques ont permis de calculer p=0.19, et ce résultat n'est pas statistiquement significatif. Le hasard aurait pu arriver à la même différence. (On n'abordera pas ici la question de "l'odds ratio" qui est indiqué entre parenthèses dans la même case, avec sa propre p-value, et qui vise à mesurer l'efficacité du traitement.)
6ème ligne : c'est le même critère qui est comparé, mais pour les patients atteint d'un Covid léger ou modéré. Aucun patient ne s'est aggravé, ni dans le groupe traité ni dans le groupe non-traité : ils ont eu le même résultat, ce qui explique la valeur la plus élevée possible pour la p-value : p=1. Cet essai ne permet de rien dire sur la capacité de la bithérapie à empêcher l'aggravation des formes légères et modérées. Ni qu'elle est utile, ni qu'elle est inutile.
7ème ligne : Pour les patients en état sévère, un seul des 11 patients du groupe traité a vu son état se détériorer, contre 6 parmi les 22 du groupe contrôle. Intuitivement, cela pourrait laisser supposer une efficacité du traitement pour empêcher l'aggravation des patients en état sévère, mais la p-value de 0,15 nous indique que statistiquement, un traitement sans effet aurait eu 15% de chances de donner un résultat aussi bon. C'est suffisamment élevé pour qu'on s'abstienne de dire que l'essai a établi l'efficacité. Mais cela ne prouve aucunement, ni même ne suggère, que le traitement a été inefficace : il semble avoir été efficace, mais le degré de certitude que ce n'était pas dû au hasard reste trop élevé.
8ème ligne : comme pour la 4ème ligne, la p-value n'a pas pu être calculée faute de patient critique dans le groupe contrôle.
Les 4 dernières lignes concernent un dernier critère : le taux de mortalité parmi les patients. Les auteurs ont comparé le nombre de décès dans chacun des groupes (traité et contrôle) et dans chacun des sous groupes correspondant à une sévérité de la maladie.
9ème ligne : avec 2 décès parmi les 70 patients du groupe traité contre 6 décès parmi les 70 patents du groupe non traité, les patients traités semblent avoir eu un meilleur sort que ceux qui ne l'étaient pas, mais la p-value de 0,14 indique que le résulat n'est pas statistiquement significatif. Les remarques formulées au sujet de la ligne 7 s'appliquent.
10ème ligne : comme pour la 6ème ligne, p=1 car aucun décès n'étant intervenu parmi les cas légers et modérés, la comparaison entre les patients traités et non traités dans le cadre de cet essai ne donne aucune indication quant à l'effet du traitement sur la mortalité des patients atteints d'un Covid léger ou modéré.
La 11ème ligne est un exemple intéressant : parmi les 22 patients admis en état sévère, 6 sont décédés, contre aucun parmi les 11 patients en état sévère traités par la bithérapie. On pourrait penser avoir là une preuve solide de l'efficacité du traitement, mais les statistiques viennent modérer cet espoir : ici, p=0,052. C'est-à-dire que on a 5,2 chances de se tromper si on affirme que le traitement est responsable de l'absence de décès dans le groupe traité. Certes 5,2% de chances, ce n'est pas énorme, mais c'est au-dessus de la barre des 5% qui est, par convention arbitraire, retenue pour distinguer un résultat significatif d'un résultat non significatif statistiquement. Ce résultat ne sera donc pas considéré comme une preuve.
Enfin, la 12ème et dernière ligne n'a pas de p-value, pour les raisons déjà évoquée pour les 4ème et 8ème lignes. Les auteurs écrivent toutefois que 2 décès sur 11 patients en état critique leur semble correspondre à un pourcentage (18,2%) très inférieur à celui qu'on observe en général chez les patients en état critique.
Au final, cette étude "prouve" qu'on guérit plus vite avec la bithérapie que sans, mais elle ne prouve pas que ce soit vrai pour des patients en état sévère ou en état critique. Elle ne prouve pas non plus que la bithérapie testée réduit le risque d'aggravation ni le risque de décès.
Pour autant, un traitement absolument efficace, qui diviserait par 3 le nombre de décès, mais testé sur 2 groupes de 70 personnes chacun, avec 2 décès dans un groupe et 6 décès dans l'autre, aboutirait à la même conclusion : absence de preuve d'efficacité...
Quelques remarques sur l'étude de Hashim et al.
On l'a utilisée ici pour illustrer le sens de la p-value et de la notion de "statistiquement significatif". Les résultats qu'elle présente sont toutefois à prendre avec prudence. En effet, cette étude ne présente pas — ou pas encore — toutes les garanties que ses résultats sont valides. En particulier, la version disponible en ligne, qui précise que les patients ont été réparti dans l'un ou l'autre groupe au hasard, simplement en fonction de la date paire ou impaire de leur prise en charge, ne donne pas de tableau comparatif sur les caractéristiques des patients de chaque groupe. On ne peut donc pas exclure que d'autres facteurs que le traitement aient conduit à une évolution différente des patients des deux groupes : l'âge des patients était-il comparable ? Y avait-il autant de comorbidités dans les deux groupes ? De tels facteurs de confusion doivent être maîtrisés pour s'assurer que le traitement est la seule différence entre les deux groupes, mais les données mises en ligne ne permettent pas de s'assurer que cela a été fait.
Peut-être est-ce lié à ce qui précède, mais il faut également noter que l'étude de Hashim et al., à la date de rédaction de ce billet, est en pré-publication ("preprint"), ce qui signifie qu'elle n'a pas encore été validée par un comité de lecture composé d'autres scientifiques (des "pairs".)
Enfin, on peut s'étonner d'un détail : sur les 96 personnes en état modéré au moment de leur prise en charge (48 dans chaque groupe), aucune n'a évolué vers une forme sévère. Se pourrait-il que le traitement standard appliqué à tous les patients, comprenant de la vitamine D, du zinc, de la vitamine C et 5 jours d'azithromycine, aide les patients atteints d'un Covid léger ou modéré à éviter l'aggravation ? Ou est-ce dû au hasard ? Il faudrait calculer une p-value...



