Il n'existe que deux méthodes pour expliquer les 3 lois de Kepler : les hypothèses de Newton et d'Einstein. Voici la troisième, qui n'est pas une hypothèse, ni une théorie, mais une simple propriété géométrique.

Vous voyez ce qu'est une rotation uniforme ? C'est un mouvement qui décrit un cercle, à vitesse constante. Et une translation uniforme ? C'est un mouvement en ligne droite, à vitesse constante. Maintenant, voyez-vous la trajectoire d'un mobile qui serait à la fois en rotation uniforme et en translation uniforme ? Non ? Alors levez les yeux au ciel : tous les astres sont de tels mobiles. C'est ce que je vais démontrer dans ce billet.
Les trois lois de Kepler
Pour commencer il faut rappeler le fondement expérimental des lois de la gravitation, de Newton, puis d'Einstein. Ce sont les lois de Kepler.
Kepler était myope, et de ce fait, il ne pouvait participer aux observations astronomiques de l'observatoire qui l'employait, celui de Tycho BraheKepler. Mais il était bon en maths. Il fut donc employé à la constitution d'almanachs, destinés à la navigation, à partir des relevés astronomiques. A force de manipuler toutes ses données, Kepler était de plus en plus persuadé d'une structure héliocentrique du monde. En revanche Tycho Brahe est toujours resté certain de la validité du modèle géocentrique de Ptolémée. Il paraît que cela provoquait fréquemment des étincelles entre les deux hommes.
C'est 8 ans après la mort de Brahe, en 1609, que Kepler publie finalement ses deux premières lois. La troisième le sera en 1619. C'est définitivement la consécration du modèle héliocentrique. Ces lois sont les suivantes :
les planètes se meuvent sur des ellipses dont le soleil est un foyer,
l'aire balayée par leur rayon depuis le soleil, en un temps donné, est la même tout au long de la trajectoire, c'est la loi des aires,
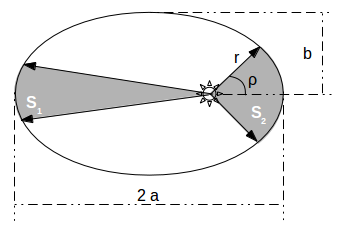
La loi des aires : les surfaces S1 et S2 sont égales, et le temps pour les balayer sont identiques.rest le rayon vecteur,ρest l'anomalie vraie, a et b sont respectivement le demi grand et le demi petit axe de l'ellipse.
le carré de la période de révolution est proportionnel au cube du grand axe de l'ellipse.
Ces trois lois sont remarquables car, depuis, elles se sont révélées exactes, non seulement pour les planètes du système solaire, mais aussi pour tous leurs satellites … et tous les astres du ciel, même les étoiles au sein des galaxies. Pour être exact, pour que ces trois lois soient formellement applicables à tous les astres de l'univers, il faut remplacer le terme « ellipse » par « conique » et le terme « soleil » par « corps central ». Ainsi énoncées, les trois lois de Kepler s'appliquent à tous les astres de l'univers, comme le théorème de Pythagore s'applique à tous les triangles rectangles de l'univers. C'est la magie de la géométrie choisie par la nature, pour fabriquer l'univers.
Deux explications seulement
Tout cela est fort lyrique, mais une question se pose alors : pourquoi la nature a-t-elle choisi les lois de Kepler, plutôt que d'autres ? Quelle est la cause de cet effet observable ?
C'est Isaac Newton qui répondra le premier à cette question, en proposant l'hypothèse de l'attraction universelle. Et personne d'autre ne fera mieux, jusqu'à Albert Einstein. Ce dernier est le second à proposer une explication des trois lois de Kepler. Son hypothèse est celle de la Relativité Générale, qui est aujourd'hui la base conceptuelle fondamentale de la cosmologie moderne. L'hypothèse d'Einstein se confond avec celle de Newton pour des vitesses faibles devant celle de la lumière, et des masses faibles, au regard de celle d'un trou noir, par exemple. Ainsi dans la grande majorité de leurs études, les astrophysiciens utilisent la méthode de Newton, qui est la plus simple à mettre en œuvre.
Quoi qu'il en soit, ce sont aujourd'hui les deux seules méthodes connues pour expliquer les lois de Kepler. Nous allons maintenant en décrire une troisième, qui n'est pas une hypothèse, mais une propriété cinématique élémentaire.
Voici la troisième
Pour des raisons que je vous expliquerai plus tard dans ce blog, j'en suis arrivé à me demander quelle est la trajectoire d'un mobile dont la vitesse est l'addition d'une vitesse de rotation et d'une vitesse de translation, toutes deux de module constant (d'intensité constante). Mathématiquement la vitesse d'un tel mobile s'écrira simplement ainsi :
v⃗ = v⃗R + v⃗ T=ω⃗ ∧ r⃗ + v⃗T avec vR=ωr=cste et vT=cste (1)
Dans cette formule v⃗ est la vitesse du mobile, v⃗R est la vitesse de rotation, v⃗T la vitesse de translation, r⃗ est le rayon vecteur joignant le foyer de la conique au mobile, et ω⃗ est la fréquence de rotation.
La figure suivante représente les vitesses caractéristiques du mouvement (1) :
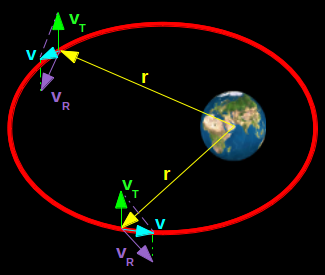
Sur cette figure d'une ellipse, sont représentées deux situations différentes pour un satellite. La flèche jaune est le rayon vecteur. La flèche turquoise est la vitesse réelle du satellite. La flèche verte est la vitesse de translationvT, toujours colinéaire au petit axe de l'ellipse. La flèche mauve est la vitesse de rotationvR, toujours perpendiculaire au vecteur rayon.
Je vais vous épargner les démonstrations, trop mathématiques, de l'étude cinématique de la relation (1), que vous trouverez en détail dans ce document, pour en arriver à ses résultats les plus importants.
Tout d'abord on montre que le mobile possédant la vitesse (1) aura une conique pour trajectoire, dont l'excentricité vaut e=vT/vR, et le paramètre vaut p=GM/vR2, où G est la constante universelle de la gravitation, et M est la masse du corps central, situé au foyer de la conique. Ainsi lorsque vT=0, la trajectoire est un cercle, c'est une ellipse si vT<vR, une parabole si vT=vR, et une hyperbole si vT>vR. Le mobile respecte donc la première loi de Kepler.
La vitesse (1) permet aussi de vérifier que le mobile aura un moment angulaire L constant. Cette constance du moment angulaire impose que l'aire balayée par le rayon, en un temps donné, soit une constante, tout au long de la trajectoire. C'est exactement la seconde loi de Kepler.
Quant à la troisième, elle n'est qu'une conséquence de la seconde. On montre aisément que pour une trajectoire elliptique, il faut vérifier la relation suivante :
LvR=4π2a3/T2 (2)
où a est le demi grand axe de l'ellipse et T est la période de révolution. Cette expression est bien celle de la troisième loi, à condition queLvR soit une constante, ce qui est bien le cas.
Ainsi un mobile dont la vitesse est donné par la relation (1) obéit aux trois lois de Kepler.
Inversement, La vitesse de tous les astres qui suivent les lois de Kepler, peut être écrite sous la forme (1).
On peut noter que la propriété cinématique (1) ne fait appel à aucune notion de masse. Elle n'est que purement géométrique. Tout comme le théorème de Pythagore s'impose, quel que soit le matériau constituant le triangle rectangle. Et cela est totalement cohérent avec le principe d'équivalence faible, celui de Galilée, dont je vous ai parlé dans mon précédent billet : dans un champ de gravitation, tous les corps se meuvent indépendamment de leurs masses.
Enfin, on remarque que l'équation (2) est bien connue des praticiens de la méthode de Newton, à ceci près que le terme physique newtonien GM est ici remplacé par le terme qui est purement cinématique. La méthode de Newton est cohérente avec la cinématique si LvR=GM.
Epilogue
Dans mon billet précédent j'ai montré que les théories de Newton et d'Einstein sont sujettes à caution, car elles respectent le principe d'équivalence, qui est s'avère expérimentalement faux. A contrario, la vitesse de tous les mobiles qui respectent les trois lois de Kepler, est donnée par l'équation (1), que les lois de Newton, et d'Einstein, soient vraies ou pas. C'est un fait géométrique qui est totalement indépendant de toute hypothèse physique, telle l'attraction universelle par exemple.
Si une hypothèse sur la gravitation est émise, quelle qu'elle soit, on comprend qu'il faudra avant tout qu'elle respecte les lois de la géométrie et de la cinématique, c'est à dire l'équation (1). Heureusement nous avons vu que la cinématique et la gravitation de Newton sont cohérentes si LvR=GM. On peut donc "espérer" ...
Mais pas trop longtemps quand même, car nous verrons, plus tard dans ce blog que, les lois de Newton ne sont plus cohérentes avec la cinématique, dans le cas de la chute des corps, et celui de la vitesse de rotation des galaxies.
HCl
Vous retrouverez cet article sur mon blog HClAtom



