Samedi-sciences (163) : comment la photo d’une robe est devenue virale

Le mois dernier, un débat métaphysique sur une robe bicolore a provoqué un phénomène « viral » sur Internet. La photo de la robe, mise en ligne par une utilisatrice de Tumblr, Caitlin McNeill, était accompagnée d’un appel que l’on peut traduire ainsi : « Les gars, aidez-moi, cette robe est-elle blanc et doré ou bleu et noir ? Moi et mes amis, on n’arrive pas à se mettre d’accord et on pète les plombs».

L’appel a déclenché un tsunami de commentaires qui n’ont pas suffi à élucider l’énigme des vraies couleurs de la robe. Un billet sur Buzzfeed qui reprenait le post de Caitlin McNeill a été vu en 24 heures par plus de 23 millions d’internautes, attirant jusqu’à 670 000 visiteurs en même temps. La fameuse robe a même inspiré l’Armée du salut en Afrique du sud, qui l’a utilisée pour illustrer une campagne dénonçant les violences contre les femmes.

Pourquoi une vidéo ou une photo diffusée sur Internet devient-elle « virale » ? Le terme qualifie un contenu qui circule rapidement sur le web, est partagé par un grand nombre d’internautes via les réseaux sociaux et devient ainsi très connu. Mais quels mécanismes sous-tendent ce phénomène de propagation de l’information ?

Une équipe de chercheurs animée par Sharad Goel, de l’université Stanford, a tenté de définir mathématiquement les propriétés de la « viralité ». Comme l’expliquent Goel et ses collègues dans un article à paraître dans Management Science, lorsque l’on dit d’un contenu en ligne – vidéo, image ou article - qu’il est devenu viral, « on entend en général pas seulement qu’il est devenu rapidement populaire, mais aussi que cette popularité est liée à un certain processus de contagion de personne à personne, analogue à la diffusion d’un virus biologique ».

L’idée de Sharad Goel est de mesurer le degré de viralité d’un événement donné, autrement dit le degré auquel il se propage par contagion. Le problème est que la plupart des événements en ligne qualifiés de viraux ne le sont que partiellement : le plus souvent, leur popularité est due à la fois à la contagion entre individus et au relais de médias à grande diffusion. Goel cite par exemple une vidéo qualifiée de virale, mais qui a été diffusée au départ sur le site de la chanteuse Taylor Swift. Cette dernière a totalisé plus de 130 millions de téléchargement de ses chansons dans le monde, et représente quasiment un média de masse à elle toute seule.

« Un contenu plus proche de ce que j’appelle viral est une chose qui n’est pas promue par une célébrité et dont on n’imagine pas a priori qu’elle va devenir très populaire, explique Goel dans un entretien avec la revue Nature. (…) C’est un contenu qui se propage principalement de personne à personne, plutôt qu’à travers des canaux de diffusion populaires tels que de grands journaux comme le New York Times. »

La communication de masse classique ne fonctionne pas sur le mode viral. Un média de masse comme une télévision ou un grand journal communique sur le principe d’une source unique qui diffuse un contenu donné vers un grand nombre de récepteurs, lesquels captent le message simultanément. Un événement télévisuel comme la Coupe du monde de football attire autant d’audience, sinon bien davantage, qu’un événement viral sur Internet, mais le mode de propagation de l’information n’est pas du tout le même dans les deux cas.

Dans l’affaire de la robe, si la dimension virale est importante, les canaux de diffusion classique ont aussi joué un grand rôle, l’histoire ayant été relayée par de nombreux journaux et autres médias de masse.

Sharad Goel distinguent donc deux situations extrêmes : celui ou un message est diffusé par une source unique et en une seule fois à un grand nombre de récepteurs (situation des médias de masse classiques) ; et celui ou le message se propage uniquement par contagion d’individu à individu à partir d’un émetteur initial, ce qui correspond au modèle viral (les deux cas sont illustrés par le schéma ci-dessous).

En général, les contenus populaires – vidéos, photos, articles, etc – doivent leur notoriété à un mélange entre ces deux modes extrêmes. De ce fait, Goel et ses collègues ne classent pas les contenus en viraux et non-viraux. Ils mesurent le degré de viralité sur une échelle continue qui va de la communication purement sur le mode médias de masse à la pure contagion sur le mode viral.

Schématiquement, la diffusion d’un contenu peut être représentée par un arbre dont les branches illustrent la circulation du message. Chaque ramification de l’arbre correspond à un émetteur et/ou un récepteur du contenu. Autrement dit, à une personne qui partage le contenu et/ou le retransmet.

A partir de cet arbre, Goel et ses collègues définissent la « viralité structurelle », qui est, mathématiquement, la distance moyenne entre deux personnes qui ont partagé le contenu. La distance dont il est question ici n’est pas une distance ordinaire, elle représente le nombre de branches qu’il faut parcourir pour relier deux individus ayant partagé le contenu. Elle s’exprime par la formule ci-dessous :

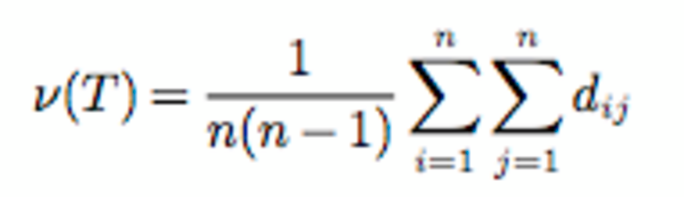
Cette formule peut paraître obscure, mais intuitivement elle signifie que plus un message a été partagé et réémis, plus il est viral. Prenons le cas le plus simple, celui où il n’y a pas de la diffusion selon le mode des médias classiques, par exemple la diffusion d’une émission sur une grande chaîne de télévision. Dans ce cas, il n’y a pas de viralité. L’arbre se ramène alors à un point correspondant à la chaîne émettrice, d’où partent autant de branches qu’il y a d’auditeurs, chaque branche aboutissant à un auditeur. Il est facile de voir qu’on peut relier deux auditeurs quelconques, disant A et B, en remontant de A à l’émetteur puis en redescendant de l’émetteur à B. Par conséquent, on a parcouru deux branches pour relier A et B, et la distance est 2. Comme cela est vrai pour n’importe quelle paire d’auditeur, la distance moyenne, ce que Goel et ses collègues appellent viralité structurelle, est aussi 2, qui correspond au minimum de viralité.

Bien sûr, l’arbre est beaucoup plus ramifié si, au bout de chaque branche se trouve un individu qui retransmet le contenu à un certain nombre d’autres, qui a leur tour le retransmettent, etc. Et plus l’arbre se ramifie, plus la distance moyenne entre deux ramifications – autrement dit la viralité selon Goel – augmente. Intuitivement, cela signifie grosso modo que plus il y a de « ré-émetteurs » du message, plus il est viral.

Les chercheurs ont utilisé leur notion de viralité structurelle pour analyser un ensemble d’un milliard de diffusions d’événements sur Twitter – notamment la propagation de nouvelles, de vidéos, d’images ou de pétitions. Il apparaît que

même sur Internet, l’information circule encore souvent sur le mode de la diffusion d’une émission de télévision classique. En moyenne, Goël et ses collègues observent que pour dix tweets, il y a seulement trois retweets.

Ils constatent aussi que globalement, le degré de viralité d’un événement n’est pas corrélé à sa célébrité. Les événements les plus notoires doivent leur célébrité à une combinaison de viralité et de diffusion sur le mode classique. Pour les vidéos et les images, les chercheurs constatent que même les plus longues cascades d’événements, dans lesquelles un post est reposté dix mille fois, n’ont qu’une viralité structurelle d’environ 3, à peine plus que le minimum de 2. Et le nombre n’est pas beaucoup plus élevé pour les nouvelles qui circulent sur le web.

En résumé, l’utilisation d’Internet et des réseaux sociaux n’a que partiellement modifié la donne par rapport aux médias de masse classiques. La transmission d’information reste fortement dépendante du mode de diffusion d’un émetteur unique vers un grand nombre de récepteur. Ainsi, les chercheurs notent que « la popularité des images et des vidéos… est probablement due aux célébrités, qui ont de plus en plus souvent des dizaines de millions de followers sur Twitter. » Le web ne serait donc pas aussi participatif qu’on pourrait le croire.