Après avoir rappelé le principe général assez visible et compréhensible nous expliquerons une stratégie de dénigrement efficace de l'hydroxychloroquine, mais plus compliquée à comprendre et que nos médias se gardent bien d’expliquer.
1°) Rappel sur la guerre médiatique
Il est évident qu’un combat acharné est mené pour gagner la bataille de l’opinion publique avec notamment un martelage sur les dangers du traitement et l’exhibition de pseudo-comparaisons affublées de l’incontournable mention « SCIENTIFIQUE »...
Ce combat est important, car malgré le martelage des médias dominants y compris Media-Part (!) qui cherchent par tous les moyens à décrédibiliser aussi bien le traitement lui-même, que le Pr Raoult (avec une plus grande discrétion sur les autres chercheurs de l’IHU), il faut bien reconnaître que l’opinion publique perçoit que quelque chose cloche.
Il est donc important d’anesthésier le grand public. Mais il faut pour cela aussi convaincre les praticiens qui sont partagés et les dissuader d’adopter un point de vue critique sur les essais et sur la stratégie d’évitement adoptée par les experts au pouvoir. Il faut aussi dissuader les praticiens de s’écarter des recommandations officielles. Le ruissellement passe aussi par les revues médicales professionnelles ...
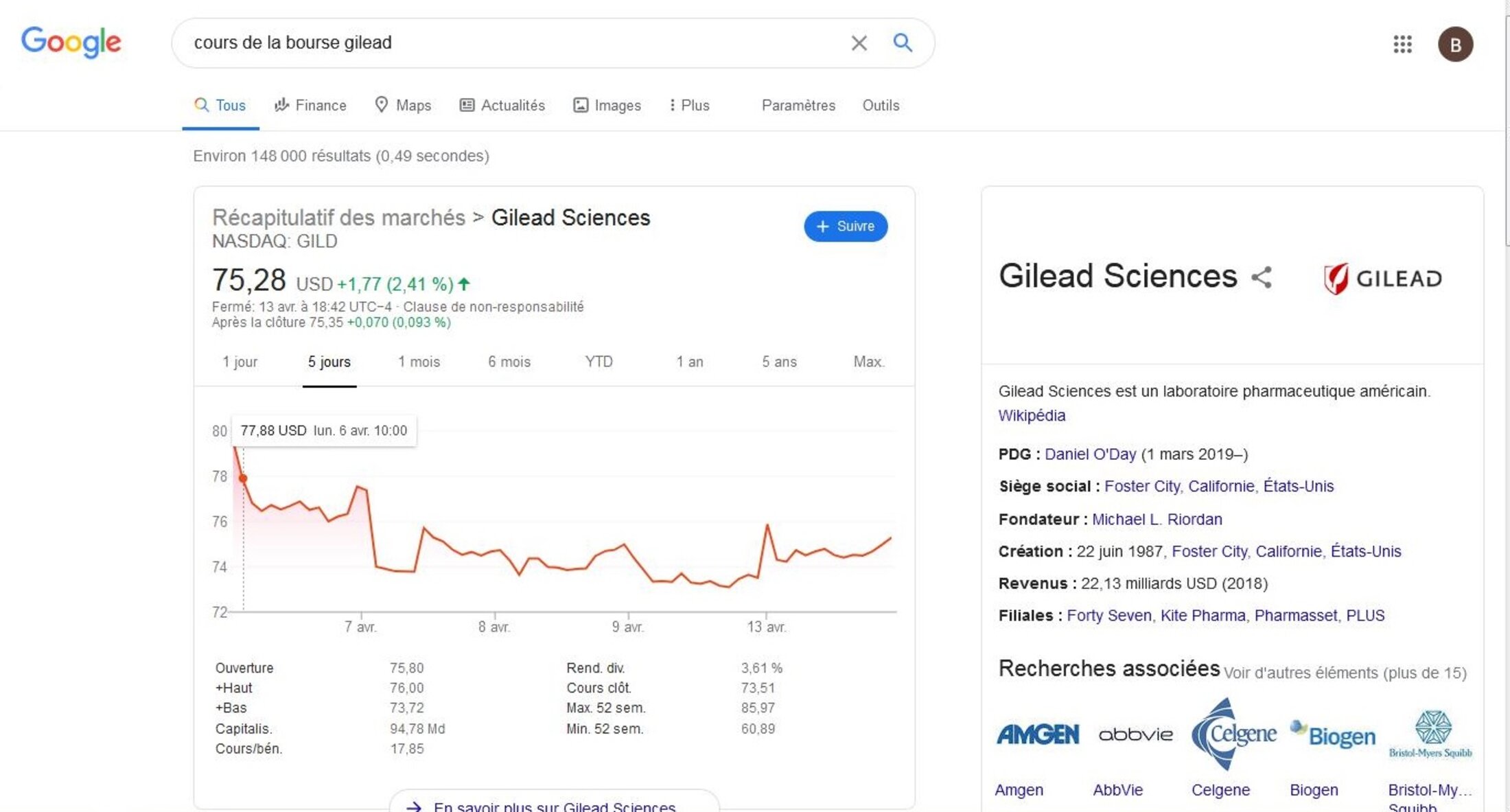
Le grand public ce sont aussi les investisseurs (lire par exemple la presse financière, regarder le cours de la bourse de Gilead en fonction des annonces etc.), les responsables politiques à tous les niveaux qui sont des pivots importants dans cette bataille d’opinion. Enfin il ne faut pas croire que ce combat ne se joue qu’au niveau national. Certes la vérité scientifique n'est pas une question d'opinion mais une supercherie scientifique à grande échelle si.
C’est une grande victoire médiatique, si à force d’informations anxiogènes, on réussit à faire stopper l’utilisation d’un médicament par un hôpital Suédois qui n’a observé que des maux de tête mais qui est soumis à des recommandations ministérielles etc. Qui va lire le détail ? ...Ou si une star se plaint de vertiges. C’est une plus grande « victoire médiatique » (pardon pour la formule), si un dosage excessif conduit à un décès. Naturellement l’information est largement relayée, si possible un peu déformée comme dans le cas d’un essai au Brésil où l’on omet de préciser que c’est un traitement surdosé (900mg/J) qui est interrompu, mais pas le traitement à (600mg/j).
L'information est parue le 12 avril dans le New York Times (By Katie Thomas and Knvul Sheikh April 12, 2020)
https://www.nytimes.com/2020/04/12/health/chloroquine-coronavirus-trump.html
Article précis et complet mais qui donne:
ou
https://www.cnews.fr/monde/2020-04-13/une-etude-sur-la-chloroquine-stoppee-au-bresil-apres-des-effets-secondaires-trop
Oh la belle remontée du cours de l'action GILEAD le 13 avril (avec un beau pic initial) ... après plusieurs jours de décroissance régulière !!!

Agrandissement : Illustration 1
On a déjà examiné la stratégie qui consiste à multiplier des comparaisons avec tout... sauf LE protocole préconisé : doses différentes, association omise, critère d’inclusion aberrant (doublés d’info mensongères cf discovery) ou simplement différence d'ancienneté dans la maladie, âge etc.
2°) Examen de la stratégie qui commence à se répandre.
Nous allons examiner une autre stratégie, déjà bien éprouvée, qui permet utilement de déstabiliser le débat ou de dissuader d’approfondir.
Il faut d’abord comprendre une subtilité des essais cliniques. En schématisant, quand on compare deux médicaments, il y a deux façons de se tromper.
La première (appelée risque de 1ère espèce) consiste à dire que les deux sont différents alors qu’ils ne le sont pas. Ainsi il peut arriver qu’une pièce de monnaie équilibrée tombe plus souvent sur face au point que l’on déclare que la différence est significative alors qu’il ne s’agit que d’un coup de malchance. La "p-value" que l’on donne dans les articles scientifiques permet de contrôler ce risque.
Une différence est dite significative quand la probabilité de ce que l'on observe est, pour des médicaments ayant un effet identique, inférieure à un seuil donné (5% ,1%, 0,1%). Par exemple, si on dit que la différence entre les deux médicaments est significative au seuil de 1% cela veut dire que si cette différence était le seulement due au hasard cela n’aurait que 1 chance sur 100 de produire.
L'autre façon de se tromper (appelée risque de seconde espèce) consiste à conclure qu’il n’y pas de différence alors qu’en réalité la différence existe.
Par exemple si une pièce de monnaie est légèrement déséquilibrée il y beaucoup de chance qu’en la lançant 60 fois on observe rien qui permette de conclure alors que si on la lance 1000 fois on sera en mesure de constater une différence significative entre le proportion attendue et la proportion observée.
Il faut comprendre qu’un test est construit pour contrôler le risque de 1ère espèce alors que le risque de seconde espèce va dépendre de l’importance de la différence entre les médicaments et du nombre de personnes testées. En d’autres termes avec 60 lancers, plus la pièce est déséquilibrée moins on a de chances de ne pas s’en apercevoir et donc de se tromper.
Pour diminuer le risque de seconde espèce il faut augmenter le nombre de personnes testées (ou de lancers de la pièce de monnaie).
Le risque d’erreur de seconde espèce est très élevé pour de petits échantillons.
Par exemple:
Si on veut comparer un traitement à un placebo. Admettons que l’on considère que la différence est significative en dessous d’un seuil de 5% et que l’on prenne 75 personnes dans chaque groupe.
On ne connaît ni la proportion théorique de patients qui guérissent avec le médicament, ni la proportion qui guérissent avec le placebo. (Cela supposerait de tester des milliers de personnes) mais faisons par exemple le calcul dans le cas où le placebo permet théoriquement de soigner 85% et le médicament permet théoriquement de guérir 95%. Cet écart est-il décelable?
Dans ce cas, un test sur deux groupes de 75 personnes a une probabilité égale à 48% de conclure (à tort) à l’absence de différence. Pour des proportions théoriques (un peu plus proches) de 85% et 91%, ce risque monte à 81%.
Si on fixe le risque de 1ère espèce à 1% c’est-à-dire que l’on est plus exigeant pour conclure à une différence alors le risque de 2ème espèce monte à 72% avec 85% contre 95% et monte jusqu'à 90% pour le couple 85% versus 91%.
Une bonne stratégie de dénigrement consiste à monter un essai avec suffisamment peu de personnes pour avoir un risque élevé de ne rien observer de significatif et clamer partout qu’il est inutile de continuer. Au pire si l’essai concluait à une différence significative, on invoquerait (à tort) la faible taille de l’échantillon, on recommanderait d’en faire un autre et comme la proba de conclure à tort à l’absence de différence est élevée, on finira rapidement pas trouver un test non concluant que l’on citera systématiquement pour semer le doute.
Avec 91% de personnes guéries allégués par le Pr Raoult et l’estimation de 85% couramment avancée on peut calculer qu'un test portant sur 2X15 personnes a une probabilité de 98% de ne rien voir!!!
Application
On pourra analyser à la lumière de ces explications le test chinois sur 25 personnes qui n’est pas concluant mais qui a un risque d’erreur qui pourrait avoisiner les 90% dans les conditions mentionnées ! On pourra aussi lire l’article de Capital à la lumière de ces précisions :
https://www.capital.fr/economie-politique/chloroquine-lautre-essai-clinique-qui-affaiblit l’espoir-dun-traitement-miracle-1365789
On peut aussi analyser l’essai Chinois qui n’utilise que l’hydroxychloroquine sur 2X 75 personnes et qui aurait encore plus de 90% de chance de ne pas détecter un écart de guérisons si les proportions théoriques étaient 85% et 92%. Or un tel écart est en réalité très important en pratique puisqu’il divise par deux le nombre de cas graves qui passerait 15% à 8%.
https://www.ibtimes.sg/hydroxychloroquine-really-game-changer-coronavirus-fight-43119
Certes la comparaison est plus technique et ne se limite pas à des proportions mais dans ce cas les incertitudes sont encore plus grandes et le risque de seconde espèce plus difficile à calculer mais la logique demeure.
On notera que l'on n'entend pas les "professionnels de la profession" hurler à l'escroquerie lorsque sont invoqués des résultats négatifs sur de si petits groupes... bien au contraire!
On pourra ainsi apprécier toute la rigueur intellectuelle du Pr Allen Cheng dans le document suivant:
https://www.newsmax.com/health-news/hydroxychloroquine/2020/04/15/id/962958/
“When testing new treatments, we are looking for signals that show that they might be effective before proceeding to larger studies,” Allen Cheng, an infectious disease physician and a professor of epidemiology at Melbourne’s Monash University told Bloomberg. “This study doesn’t show any signal, so it is probably unlikely that it will be of clinical benefit.”
En d'autres termes "circulez il n'y rien a voir"...
Ne pas oublier que l'hydroxychloroquine seule a un effet limité et que ce qui est préconisé par le Pr Raoult est une association.
NB Même de grands médecins ne comprennent pas la dissymétrie entre les deux risques: déceler une différence à tort / ne pas déceler une différence à tort. Si une pièce de monnaie tombe 1 fois sur pile en 11 lancers, c'est un très petit échantillons mais le résultat est très significatif (risque de déceler un déséquilibre à tort, inférieur à 1/100). Inversement avec 100 lancers, en mettant en œuvre un test peu exigeant (seuil de 5%) il y a encore un chance sur deux de ne pas déceler qu'une pièce de monnaie est déséquilibrée au point d'avoir (théoriquement) seulement 1 chance sur 10 de tomber sur pile . Avec un test plus exigeant (seuil de 1%) le risque de ne rien voir monte à 72%.
Retenir: pour une taille des groupes donnée, plus le risque de 1ère espèce est faible plus grand est le risque de 2ème espèce.
Pour de petits groupes ce risque de seconde espèce est très élevé.
La multiplication de petits tests non significatifs n'a aucun intérêt scientifique. Ils servent seulement à discréditer le traitement en cause.
En d'autres termes si quelques personnes fouillent une rivière sans rien trouver ça ne prouve pas grand chose mais si une personne trouve une pépite cela signifie qu'il y a quelque chose... mais attention si l'on multiplie trop les petits tests on finira par obtenir un évènement déclaré significatif à tort: une pierre brillante qui n'est pas de l'or en quelque sorte . En termes médiatiques c'est sans conséquence: le faux significatif sera noyé dans la masse. En termes scientifiques ça devient compliqué de s'y retrouver. Il est donc nécessaire de faire des tests sur des grands groupes pour mettre en évidence une absence de différence significative avec un faible risque d'erreur et ne pas conclure hâtivement quand un test est non significatif sur de petits groupes.
Un test significatif sur un petit groupe doit inciter à confirmer sur un plus grand groupe car si le risque d'erreur est faible il n'est pas négligeable (à 5% par exemple) mais un test non significatif sur un petit groupe ne doit pas dissuader de continuer le test sur un grand groupe.



