
Hier, 31 mars, je vous ai posé un lapin ! J’avais promis plusieurs trucs, chuis mêm’pô v’nu. La faute à la fonction round() de Python (je crois que dans d’autres langages, c’est pareil). Cette macronne confond : même si on lui dit deux décimales, elle arrondit 6.001 à 6.0 ! 6.0 ! J’vous jure. C’est un phénomène plus ou moins normal : y a que ces dingues de profs de maths et de physique qui attachent de l’importance à distinguer 6.0 et 6.00 … (ça c’est juste des points de suspension).
Enfin pas que. Si on fait des maths, quels que soient les domaines où on les applique, de la compta jusqu’à l’astrophysique, on doit parfois attacher une importance particulière à zéro, à l’arrondi, et à l’infini. Aux infinis. Alors sur mon forum, on m’a recommandé « le module décimal ».
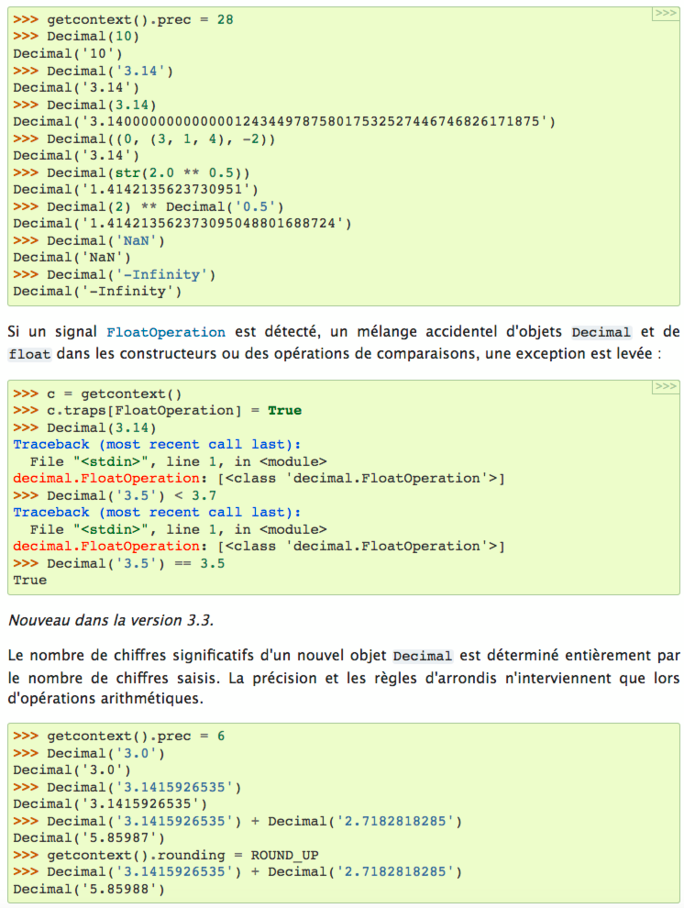
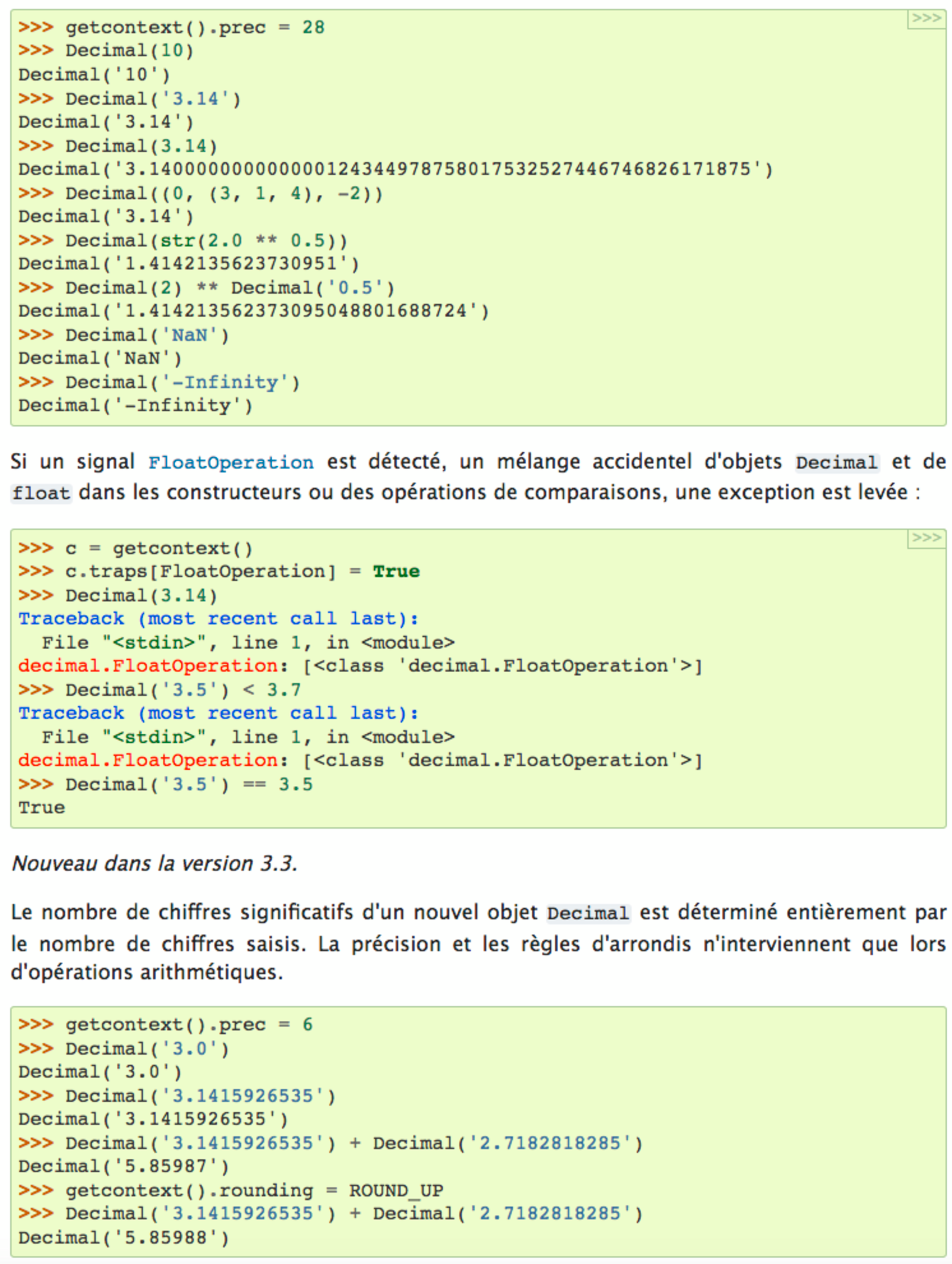
Le module decimal fournit une arithmétique en virgule flottante rapide et produisant des arrondis mathématiquement corrects. Il possède plusieurs avantages en comparaison au type float :
Le module decimal « est basé sur un modèle en virgule flottante conçu pour les humains, qui suit ce principe directeur : l'ordinateur doit fournir un modèle de calcul qui fonctionne de la même manière que le calcul qu'on apprend à l'école » -- extrait (traduit) de la spécification de l'arithmétique décimale.
Les nombres décimaux peuvent être représentés exactement en base décimale flottante. En revanche, des nombres tels que 1.1 ou 1.2 n'ont pas de représentation exacte en base binaire flottante. L'utilisateur final ne s'attend typiquement pas à obtenir 3.3000000000000003 lorsqu'il saisit 1.1 + 2.2, ce qui se passe en arithmétique binaire à virgule flottante.
Ces inexactitudes ont des conséquences en arithmétique. En base décimale à virgule flottante, 0.1 + 0.1 + 0.1 - 0.3 est exactement égal à zéro. En virgule flottante binaire, l'ordinateur l'évalue à 5.5511151231257827e-017. Bien que très proche de zéro, cette différence induit des erreurs lors des tests d'égalité, erreurs qui peuvent s'accumuler. Pour ces raisons decimal est le module utilisé pour des applications comptables ayant des contraintes strictes de fiabilité.
Le module decimal incorpore la notion de chiffres significatifs, tels que 1.30 + 1.20 est égal à 2.50. Le dernier zéro n'est conservé que pour respecter le nombre de chiffres significatifs. C'est également l'affichage préféré pour représenter des sommes d'argent. Pour la multiplication, l'approche « scolaire » utilise tout les chiffres présents dans les facteurs. Par exemple, 1.3 * 1.2 donnerait 1.56 tandis que 1.30 * 1.20 donnerait 1.5600.
Contrairement à l'arithmétique en virgule flottante binaire, le module decimal possède un paramètre de précision ajustable (par défaut à 28 chiffres significatifs) qui peut être aussi élevée que nécessaire pour un problème donné :
Ça avait bien commencé ! Ce préambule me plaisait.
Mais regardez cette petite capture :
Agrandissement : Illustration 2
J’ai remis à plus tard.
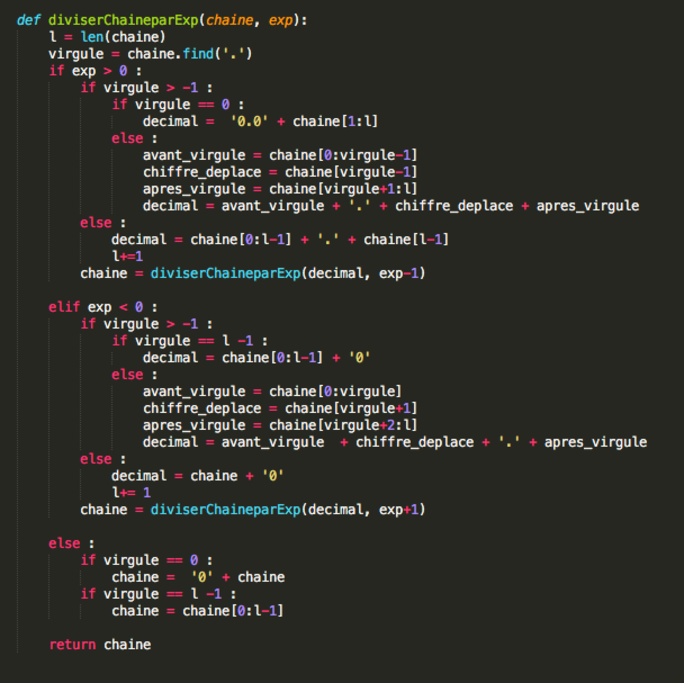
Et j’ai programmé une tiote fonction perso qui divise par des puissance de 10 (nécessaire pour mon autre fonction qui donne l’écriture scientifique en utilisant le logarithme). Mais ma division, c’est une division sur la chaine de caractères qui représente le nombre. Car je n’ai pas besoin du nombre lui-même, que j’ai déjà, même s’il n’est pas arrondi comme je voulais.
Autre capture pour vous montrer ma fonction.
Agrandissement : Illustration 3
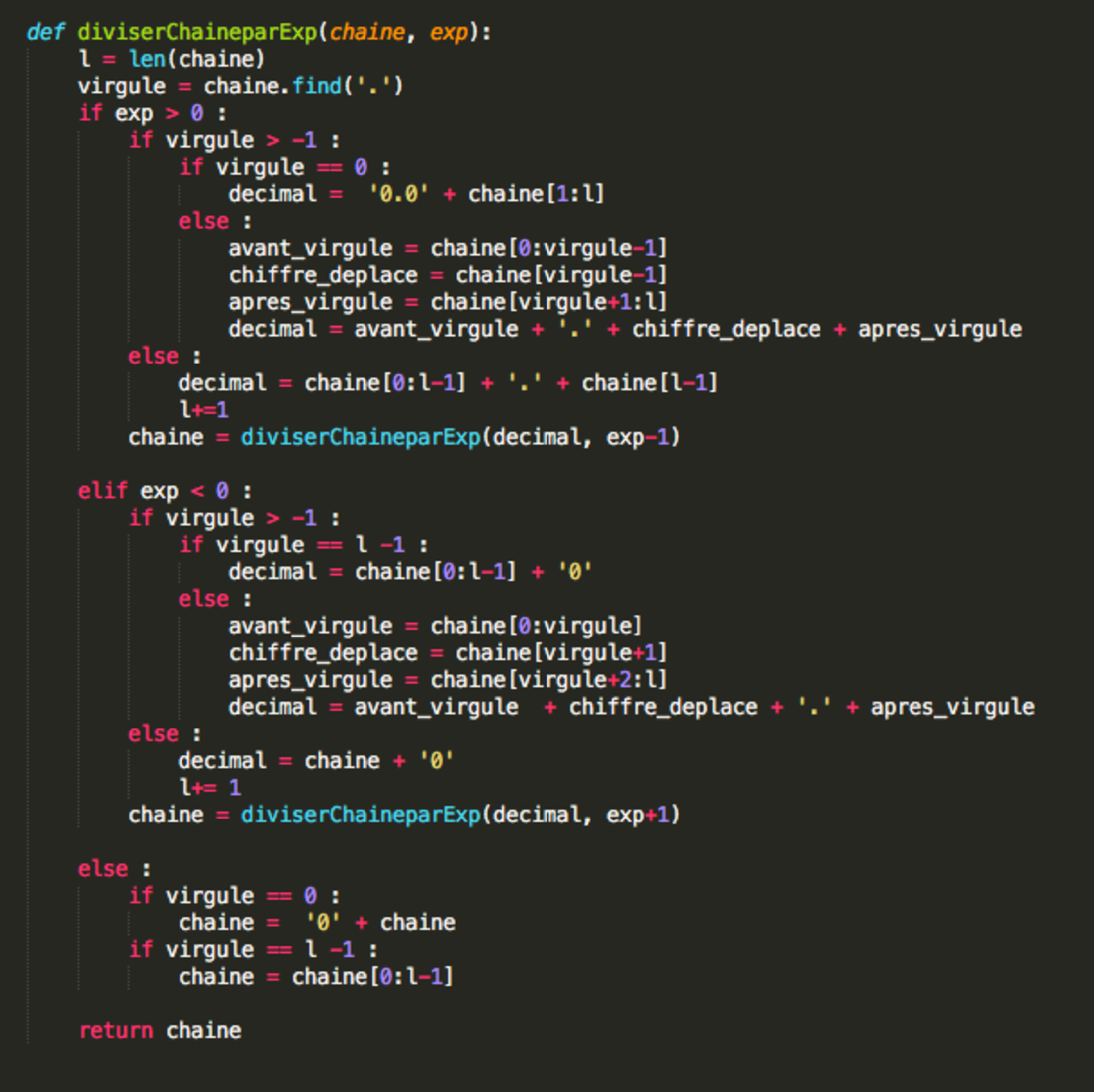
S’il y en a qui étudient l’informatique, ça va peut-être leur plaire. On lui donne une chaine de caractère telle que ’456.80456000’ et la puissance de 10 par laquelle on veut la diviser, par exemple 7. Elle doit donc retourner ‘0.000045680456000’. Ce qu’elle fait ! J’y ai passé la journée. (Hier, c’était le topo sur Pythagore qui va accompagner la première livraison mensuelle de mes cent-mille milliards de problèmes !
Donc pour demain, le début des 10¹⁴ poèmes. Avec des arrondis pile-poil. Enfin je l'espère.
Pour l’instant, la correction du lapin d’avril, pour les CE ! C'est là
Et encore un peu de maths :
Au moyen du théorème de Pythagore, exprimez :
1) La diagonale d’un carré en fonction de son côté ;
2) La diagonale d’un cube en fonction de son côté (on utilisera le résultat précédent, dans une figure plane joignant deux arêtes opposées du cube) ;
3) La hauteur d’un triangle équilatéral en fonction de son côté ;
4) En utilisant le résultat du 1), le sinus et le cosinus de 45 °;
5) En utilisant les résultats du 3), le sinus et les cosinus de 30° et de 60°.
Certaines démonstrations et calculs préliminaires peuvent être nécessaire par ci par là.



