Papa rat a mangé le sixième du fromage.
Maman, en prenant les 2/6 de ce qui restait, prend les 2/6 de 5/6 (puisque Papa a pris en quelque sorte une part sur 6, il en restait 5).
Les 2/6 de 5/6, c’est une multiplication de fractions. En règle générale, une fraction appliquée à une quantité, c’est la multiplication des deux nombres. Vérification avec par exemple : la moitié de 100 : 1/ 2 de 100. C’est bien 1/2 x 100.
Donc le repas de maman, c’est 2/6 x 5/6.
Multiplier les fractions, même quand elles ne sont pas au même dénominateur, c’est facile. On multiplie entre eux les numérateurs, on multiplie entre eux les dénominateurs. Cependant, il est astucieux de simplifier, le cas échéant, avant de multiplier. Ici c’est le cas, car il y a un 2 en haut et 6, un multiple de 2, en bas :
2/6 x 5/6 = (2 x 5 )/ (2 x 3 x 6). Il y a un 2 en haut et en bas, donc ils se simplifient.
Et la part de maman est donc égale à 5/18 du fromage.
Ensuite, ça se complique ! Car il faut ajouter les parts de papa et maman pour calculer la fraction que ça représente. Et les deux fractions ne sont pas au même dénominateur (pour ajouter, c’est galère, les fractions doivent être au même dénominateur).
1/6 + 5 / 18 !
Il faut chercher le plus petit multiple commun aux deux dénominateurs. Ça va encore, car là, l’un des dénominateurs, 18, est multiple de l’autre. Donc c’est carrément lui, le ppcm.
On va changer l’expression du quotient 1/6, en multipliant numérateur et dénominateur par 3 : 1/6 = (1x3)/(6x3) = 3/18
Ensuite, pour ajouter on applique la règle : on ajoute les numérateurs, on laisse inchangé le dénominateur. On ajoute les fractions (au même dénominateur) comme n’importe quelle chose, n’importe quel objet portant un nom : trois et cinq poires, ça fait huit poires. Eh bien 3 dix-huitièmes et 5 dix-huitièmes, ça en fait 8 aussi.
Papa et maman ont donc laissé 8/18. Cela se simplifie, en faisant un peu le contraire de ce qu’on a fait tout à l’heure pour mettre au même dénominateur :
8/18 = (2 x 4) / (2 x 9) = 4 / 9. Les deux gros rats ont mangé l’équivalent de quatre parts sur neuf. Ils en ont donc laissé cinq. Ils ont laissé 5/9.
Fifille arrive et boulotte la moitié de ces 5/9. Comme tout à l’heure, facile :
1/2 x 5/9 = (1x5) / (2 x 9) = 5 / 18. Fifille a mangé comme maman !
De nouveau, il faut ajouter les trois repas précédents :
1/6 + 5 / 18 + 5 / 18 = (3 + 5 + 5) / 18 = 13 / 18. Il reste donc 5 morceaux sur 18. C’est logique : comme elle a mangé la moitié de ce qu’il y avait, la part qui reste est égale à ce qu’il y avait.
Grand gars arrive et se tape les 4/6, donc les 2/3 de ces 5/18 :
2/3 x 5/18 = (2 x 5) / ( 3 x 18) se réduit : (2x5) / (2x27) = 5/27
Somme des quatre repas : 1/6 + 5/18 + 5/18 + 5/27. Le ppcm de 6,18,27 est 54.
Donc : (1x9 + 5x3 + 5x3 + 5x2) / 54 = 49 / 54. 54 - 49 = 5, il reste 5/54
Tiot se tape les 5/6 de ces 5/54 : (5x5) / (6x54) = 25/324.
Somme des cinq repas : 1/6 + 5/18 + 5/18 + 5/27 + 25/324.Le ppcm est 324 ! 324 = 18 x 18, et aussi 12 x 27, et aussi 6 x 54
Donc 1x54 + 2x5x18 + 12 x 5 + 25) / 324 = 319/324. 324 - 299 = 5. Il ne reste que 5/324 pour la Tiote.
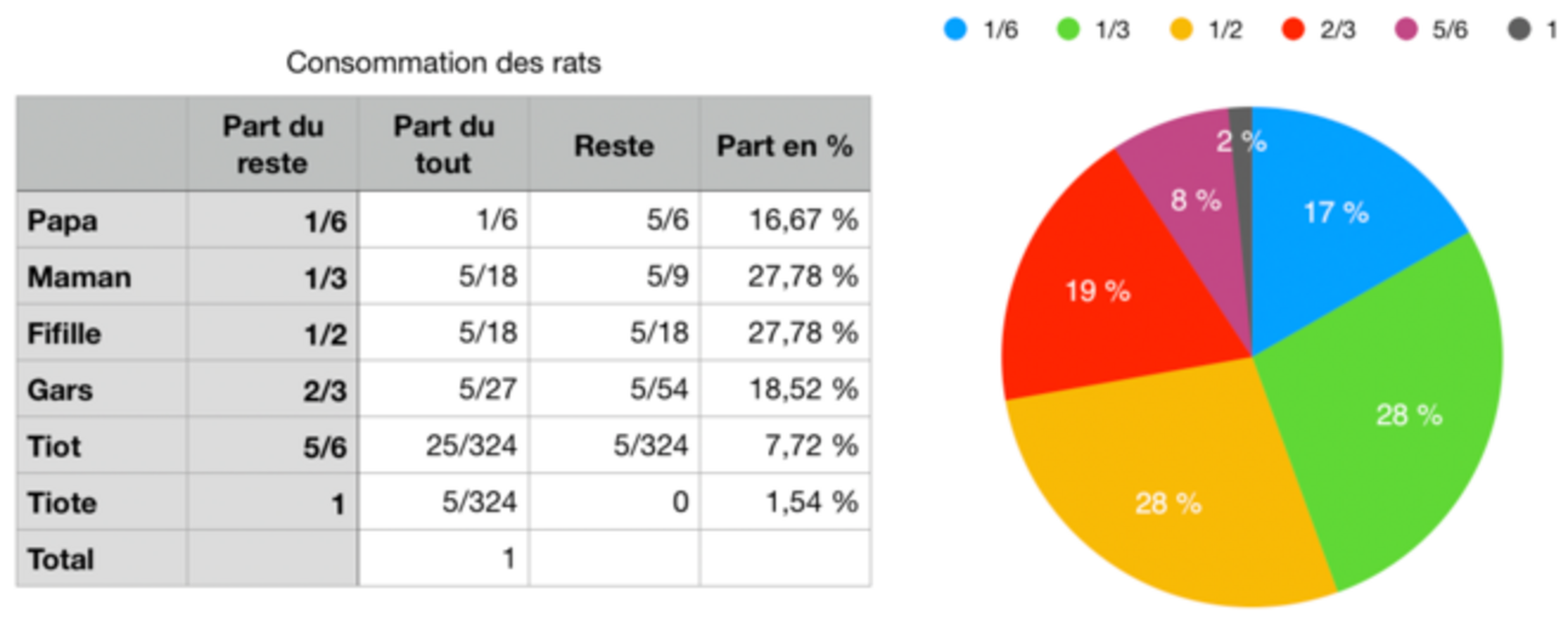
Voici le tableur et le camembert, tout à fait à propos, faits par Chapo. Merci à lui.
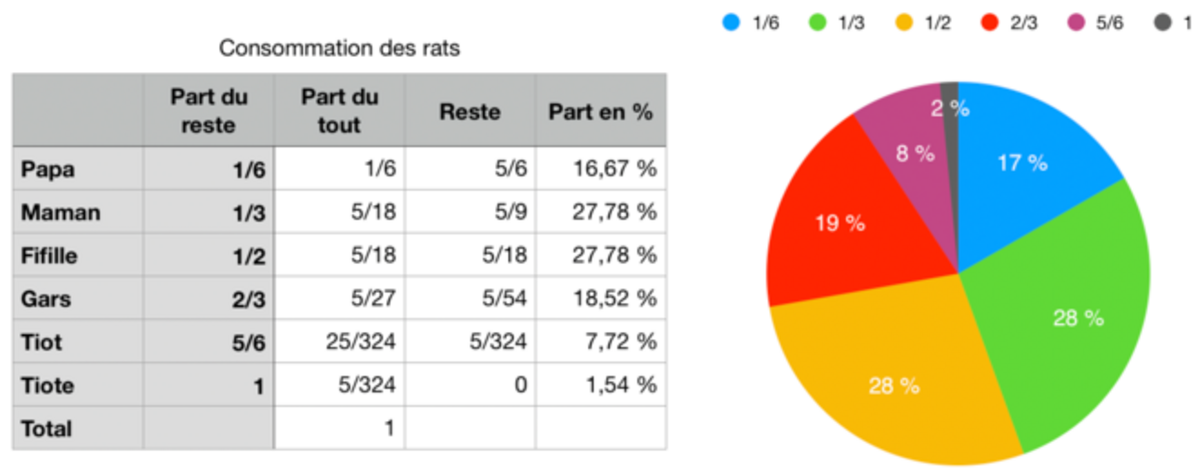
Agrandissement : Illustration 1