Introduction aux Algorithmes récursifs
Pour la rentrée, retour aux algorithmes. Rappelons qu'un "algorithme" c'est simplement une "recette de cuisine" permettant d'effectuer un calcul plus ou moins complexe. Les algorithmes sont devenus d'une importance décisive en informatique et dans le monde numérique qui est maintenant le notre, mais ils existent depuis trés longtemps, et on en a une connaissance intuitive, ne serait ce qu'à l'école ou on nous apprend à effectuer des additions et des multiplications. C'est d'ailleurs le processus de calcul d'une multiplication tel qu'on nous l'apprend à l'école qui a donné le mot "algorithme" (le livre expliquant à la fin du moyen age cette opération s'appelait "Algorithmus", du nom du mathémacien irakien Al Khwarizmi)
Nous allons voir comment fonctionnent une grande catégorie d'algorithmes, les algorithmes récursifs. Utiliser la récursivité c’est programmer une fonction qui fait appel à elle-même. La récursivité est une technique qui conduit à des solutions élégantes aux problèmes qui sont difficiles à programmer à l’aide de boucles simples.
A l'origine, on n'avait imaginé que de mettre en oeuvre une approche "ittérative". Celle ci utilise un systéme de "boucle" Dans la formalisation habituelle des algorithmes, on utilise deux sortes de boucles : les boucles "tant que"
Tant que (telle condition)
faire (tel traitement)
et les boucles "pour" donc l'exécution dépend de l'évolution d'un paramétre (en général un nombre entier)
Pour (compteur de 1 à 10000)
faire (tel traitement)
La récursivité permet de ne pas utiliser de structute de boucle. Il faut de toute façon un controle final sinon votre programme sera sans fin (ce que l'ordinateur, qui n'a pas du tout le sens de l'humour, risque de ne pas apprécier du tout)
exemple d'une fonction récursive "sans fin" :
Fonction Double (nombre) :
nombre= double (nombre) *2
Vous ne pouvez mettre fin a cette fonction qu'en utilisant "l’arrêt d'urgence" de l'ordinateur (ou en le redémarrant "à la barbare")
La fonction récursive ressemblera plutot à
Fonction double (nombre)
Si nombre = 0
mettre fin au programme
nombre= double(nombre-1) *2
Tout problème résolu de manière récursive peut être résolu avec des itérations non-récursives. Tout dépend alors de la nature du probléme à résoudre. La récursivité est très efficace pour une série de problèmes (par exemple tout ce qui concerne le parcours systématique d'un arbre (structure logique) par exemples les répertoires des fichiers d'un ordinateurs, le jeu des tours de hanoi ou la programmation des fractales)
La décision d’utiliser la récursivité ou l’itération doit être fondée sur la nature et votre compréhension du problème que vous essayez de résoudre. La règle de base est d’utiliser selon l’approche peut mieux développer une solution intuitive qui reflète naturellement le problème. Si une solution itérative est évidente, l’utiliser sera généralement plus efficace qu’une solution récursive.
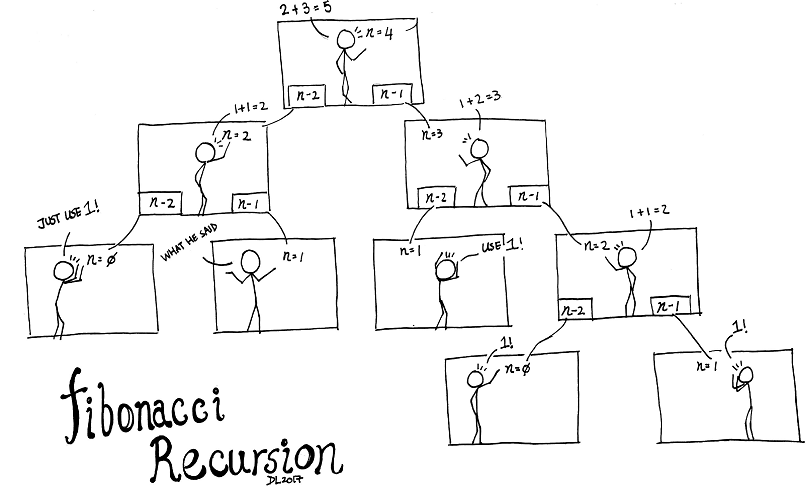
Un exemple : utiliser (ou pas) la récursivité pour calculer la suite de Fibonacci
Rappelons que nous avons vu la "suite de Fibonacci" qui se rencontre "dans la nature" (par exemple le nombre de pétales d'une fleur suit souvent la progression d'une suite de Fibonacci) Je rappelle que la suite de fibonacci consiste a rajouter les deux derniers nombre de la suite en partant de (0,1)
0,1
0,1,1
0,1,1,2
0,1,,1,2,3,
0,1,1,2,3,5
0,1,1,2,3,5,8
0,1,1,2,3,5,6,13
etc etc etc
Premiére méthode : ittérative : m
n = int(input("What Fibonacci number would you like to find? "))
def fib(n):
def fibo_
it(i): a,b,
cpt=0,1,0
while cpt <= i:
if cpt < 2 :
c = cpt
else :
c=a+b a=b b=c cpt+=1
return c
Deuxiéme méthode :
def fib(n):
if n < 2:
return n
else:
return fib(n - 1) + fib(n - 2)
On voit assez clairement que la seconde méthode semble "plus simple" que la premiére. Mais un des problémes appporté par la récursivité est que "l'élégance" de la solution se paie souvent au prix de l'efficacité (en tant que "durée d'exécution")
Ci dessous une vidéo glanée sur le site "grand public" de l'INRIA (institut de recherche informatique et automatisme) sur un probléme typique des algorithmes récursifs : les "tours de Hanoï"
Ce jeu consiste a jouer avec des plateaux et des piquets : les platteaux sont de tailles croissantes et s'enfilent sur les piquets. Il consiste a disposer tous les plateaux sur une des tiges, et a tenter de le passer d'une tige sur sur une autre avec une règle impérative : un plateau plus grand ne peut pas être placé sur un plateau plus petit
Ce casse tête assez ancien peut être résolu en utilisant l'informatique (et un algorithme récursif) plus particulièrement quand le nombre de plateau et de piquets

Agrandissement : Illustration 2

La scientifique du mois : Henrietta Swan Leavitt :

Dans notre rubrique "le machisme dans les sciences, nous allons parler une nouvelle fois d'une scientifique injustement oubliée. Celle ci est Henrietta Swan Leavitt (1868 1921). Pourtant elle a apportée une contribution essentielle à l'astronomie au XX° siécle, puisque c'est elle qui découvert la méthode qui nous a permis de calculer la distance nous séparant des autres galaxies.
Elle commença a travailler à l'université de Havard comme calculatrice (les calculs en astronomie en l'absence d'ordinateur nécessitant des "petites mains" choisie en général chez des femmes) avant de devenir astronome a part entière (avec bien des difficultés due au machisme assumé régnant alors dans l'université) Elle se spécialisa assez vite dans les "étoiles changeantes", dont la variation de luminosité apparaît comme brutale et soudaine (contrairement par exemple à notre Soleil dont la luminosité est a peu prêt constante)
Mais c'est en s'intéressant a un type particulier d'étoiles variables, les céphéides que Henrietta Swan Leavitt va faire une découverte fondamentale. en établissant une relation entre la variation de leur luminosité et leur période : « Une ligne droite peut facilement être dessinée entre les deux séries de points correspondant au maximum et au minimum, montrant qu'il y a une relation simple entre la luminosité des variables et leurs périodes. » expliquait elle. Après la mort de Leavitt, Edwin Hubble repéra des céphéides dans la nébuleuse d'Andromède et put ainsi en déterminer la distance, bien plus grande que ce que l'on pensait, faisant de cette nébuleuse une galaxie.
Henrietta Swan Levitt a été la victime expiatoire de Edward Pickering, illustre astronome au début du XX siécle. Ce fut lui qui l'employa comme "calculatrice" ainsi que maint autres femmes (on parlait à cette époque du "harem de Pickering" avec cette alliance d'outrecuidance et de machisme qui n'a malheureusement pas encore totalement disparu) et qui lui a également interdit de poursuivre ses recherches sur les Céphéléides Sur les "calculatrices de havard" on peut lire avec profit l'article de wikipedia
On peut lire un ouvrage passionnant sur ces femmes oubliées (d'ou est tiré l'essentiel de mes informations) :
Yael Nazé L'astronomie au féminin CNRS Editions 2014 192 pages
On ne se dégonfle pas !
Très dernièrement, on a beaucoup parlé des exploits d'un des inventeurs d'une solution aux problèmes posés par le "jet-pack", cette "solution de transport individuel existant depuis les années 60 consistant en une tuyère à gaz propulsant un individu. C'est à un autre moyen de transport que je vous invite à vous intéresser : le ballon de baudruche !
Tout le monde il me semble a déja eu un "ballon de baudruche" dans sa jeunesse (mais on en a souvent épuisé tous les plaisirs, l'age de raison venu) mais on ne voit pas trop l'intéret de ce genre de dispositif. Bien a tord puisque ce type de ballon est maintenant utilisé assez massivement dans les mesures météo sous forme d'un ballon sonde qui permet de mesurer les différents paramètres jusqu'a la limite de l'athmosphére

Il existe différentes sortes de ballons sondes (ballons pressurisés, ballons à infrarouge, ballons captifs) mais les ballons sondes "conventionnels" ressemblent grosso modo aux ballons de baudruche de notre jeunesse : gonflés à l'héliums et constitué de matiéres plastiques conventionnelles (néopréne, latex, etc) il se distend jusqu'a éclater en général à une hauteur comprise entre 10 et 35 Kilométres. Il est ensuite récupéré dans la mesure ou il embarque un gps (qui permet de connaitre sa position précise) et un parachute automatiquement déployé après son éclatement
Les autres dispositifs (qui n'éclatent pas) permettent d'envisager des missions de longue durées (de quelques jours à plusieurs mois)
L'équipement emporté pése en général de 10 à 35 KG -à la hauteur de la mer...
Une page élaborée par la météo nationale fourni une présentation pédagogique des ballons sondes : http://tpe-meteo-stjo.e-monsite.com/pages/ballon-sonde.html
On peut également penser transporter un individu en utilisant plusieurs ballons de baudruche. Evidemment il parait plus rationnel d'utiliser des "ballons à l'air chaud" qu'on peut plus facilement faire monter et descendre. Mais le ballon de baudruche à ses adeptes, qui utilisent une petite sarbacanne (pour percer les ballons)
Mais ce n'est pas ces ballons là qui peuvent le plus nous amuser. Parlons plutot des ballons utilisé dans le dessin animé "la haut" des studios pixar réalisé en 2009.
On rappelle le "pitch" de l'histoire : Carl vieillard bougon promis au foyer pour personnes agées s'évade avec l'aide d'un jeune scout grace a des milliers de ballons de baudruche que ce dernier a disposé autour de la maison
les ballons de lahaut

Tout le monde s'est posé la question : est ce vraiment possible ? Certains ont meme tenté l'expérience comme vous pouvez le constater vous même ci dessus mais peu ont essayé réellement de tenter l'expérience dans des conditions vraiment réalistes.
Evidemment, les mathématiciens et quelques physiciens fous (ça existe) se sont lancé dans des calculs trés compliqués afin de résoudre le probléme. Et ce qu'ils ont découvert est intéressant (et justifie à lui seul l'écriture de ce sujet à l'intérieur des "miscellannées")
En prenant pour poids moyen d'une maison américaine celui de 50 tonnes (les maisons américaines sont en général bien plus légéres que celles construite en europe) il aurait fallu plus de 100000 ballons de baudruche pour pouvoir soulever la maison.
C'est d'aeilleurs ce qui est représenté sur le shéma ci dessous ou on peut constater que la surface réelle de ballon (en gris foncé) est bien plus importante que celle qui a été représentée (en gris clair) pour servir de modéle au dessin animé

Référence : Jean Michel Courty La physique surprise Belin pour la science 2007 pages 14-17
La découverte du mois : des arbres menacés

On parle beaucoup de la disparition annoncée d'espèces vivantes emblématiques comme des mammifères comme les grands fauves, les éléphants d’Afrique, les baleines. On commence également à parler de la disparition annoncée (sur le siècle) de l'ensemble des insectes. Une autre sorte d’êtres vivants s'est rajoutée à la liste macabre : on estime maintenant que 40% des arbres en Europe pourrait disparaître, en particulier des espèces emblématique du continent comme le marronnier. Plus de 58% des espèces endémiques d'arbres seraient ainsi menacées (on appelle "espèce endémique" une espèce existant uniquement sur un continent ou un pays) dont 12% sont déclarées en état de "péril imminent"
C'est l'UICN qui a sonné le tocsin L'UICN c'est l'organisation mondiale pour la conservation de la nature. « Les arbres sont essentiels à la vie sur Terre et les arbres européens, dans toute leur diversité, constituent une source de nourriture et un abri pour d’innombrables espèces animales (…) et jouent un rôle économique clé », a déclaré Craig Hilton-Taylor, chef de l’unité « Liste rouge » de l’UICN, dans un communiqué.
Le site de l'UICN France : https://uicn.fr/
La liste rouge de l'UICN concernant les arbres : https://portals.iucn.org/library/sites/library/files/documents/RL-4-026-En.pdf
Article du monde sur le sujet : https://www.lemonde.fr/planete/article/2019/09/27/plus-de-40-des-especes-d-arbres-presentes-en-europe-menacees-d-extinction_6013312_3244.html
Le livre du mois : le kama sutra des demoiselles

Rien de salace dans cet ouvrage malgré un titre qui fleure bon l'enfer de nos bibliothèques Mais il n'en reste pas moins qu'il s'agit un livre tout a fait réjouissant, qui contient une tonne d'anecdotes toutes plus surprenantes, enrichissantes, éclairantes les unes que les autres sur ces étranges animaux qui nous entourent, d'autant plus surprenant que nous les côtoyons tous les jours : l'auteur vous parlera de ces escargots qui font de la musique avec leur narine, des soûlographies des chevreuils, et autres mystères plus surprenant encore !
présentation de l'éditeur :
Inutile de partir en safari aux quatre coins de la planète : le monde animal que nous côtoyons recèle des trésors fabuleux. Il suffit de regarder et d'écouter... Dans nos maisons, nos jardins, en ville, en forêt ou en bordure de chemin, partout où nous pouvons nous promener, se cache un bestiaire aux trésors fantastiques. Même le chat, le chien ou le moineau, apparemment si familiers, nous réservent de grandes surprises.
Au cours d'une visite guidée vivante et surprenante, ce livre plein d'humour nous révèle les secrets des petites et des grosses bêtes qui nous entourent. Racontées comme des histoires extraordinaires, illustrées de dessins de l'auteur et de photos en couleurs, voici les dernières découvertes des scientifiques et des observateurs de terrain.
Et Toujours, les jeux :
Se prendre pour Sherlock Holmes
Dans un reccueil de ses nouvelles, Sir Arthur Conan Doyle fait ainsi parler son héros :
"y a t il un point sur lequel vous désirez attirer mon attention ? '"
"oui, sur l'incident curieux du chien pendant cette nuit là"
"mais le chien n'a rien fait pendant cette nuit !"
"Justement, c'est cela qui est curieux...."
voila une suite
1,2,4,7,8,11,14,16,17,19,22,26,28,29,41,44
Considérant le dialogue entre Sherlock Holmes et le Docteur Watson, quel est le nombre qui suit
Halloween = Noel ?
Pourquoi pour les informaticiens, Hallowween = Noel ? p 27
On se lance dans la vente de bracelets !
Deux copines Anabelle et Cyntia se lancent dans la vente de Bracelets. Chacune dispose d'un stock de 30 bracelets Annabelle les vend 10€ les deux tandis que Cyntia les vend 20€ les trois Elles gagneront dont (si elles vendent toutes deux leur stock) 150 + 200€ = 350€. Mais comme ce sont de bonnes copines, elles décident de les vendre ensemble à 30 € les cinq. Elle ont donc potentiellement gagné 360€ L'amitié paie
En face de ces deux copines, deux autres nommée Christine et Daphnée décident elles aussi de se lancer dans la vente de colifichets : elles achétent elles aussi un lot de 30 bracelets. Christine les vend 10€ les deux (comme Annabelle) alors que Daphnée casse les prix avec une proposition de 10€ les trois bracelets (moitié prix que ce que propose Cyntia) Elles décident elles aussi de mettre leurs emplettes en commun en les vendant 20€ les cinq : serait ce vraiment une bonne idée ? Justifiez votre choix.
Ces trois énigmes sont tirées d'un petit ouvrage (à 3€) de Ian Stewart "Petites énigmes mathématiques et logiques" en Librio



