La théorie des groupes

La théorie des groupes est une des théores mathématiques ayant "essaimée" dans un nombre impressionnant de discipline : elle est utilisée en physique, chimie, informatique théorique, anthropologie (Claude Levi Strauss en fait une utilisation remarquée dans "Les structures élementaires du mythe", un des articles les plus remarqués de son "Anthropologie structurale")
Elle a été imaginée par un jeune mathématicien de la période révolutionnaire, Evariste Galois, disparu à l'âge de 21 ans suite à un malencontreux duel. Sa vie a été un véritable roman, et lui même fut un éternel révolté contre l'ordre social mais aussi l'ordre intelectuel de son temps, en particulier dans l'enseignement. Ayant raté son concours d'entrée a Polytechnique (qui était a l'époque la grande école "républicaine") il s'opposa trés vite à l'ordre des mathématiciens de son temps.
Son sujet de recherche principal consistait dans la recherche des solutions aux équations polynomiales d'ordre supérieur à 4 Chaque lycéen sait maintenant traiter des équations "du second degré". On sait également (mais c'est plus difficile) traiter des équations d'ordre trois (du genre 5x3 + 8x2 - 3x +2 mais en général on ne sait pas traiter les équations d'ordre égal ou supérieur à 4
Galois va avoir une intuition géniale : ce qui compte ce ne sont pas "les calculs" en tant que tels, mais les structures C'est ainsi qu'il va mettre au point la notion de "groupe"
Un groupe est un ensemble d'éléments, munis d'une "loi de composition interne" (une opération) Cette opération possède les qualités remarquables suivante : elle est "associative" (c'est a dire que l'ordre dans lequel on effectue l'opération importe peu) elle possède un "élément neutre (un élément qui fait que l'opération ne transforme pas la valeur du résultat : On peut citer l'ensemble des nombres entiers, avec comme "loi de composition interne" 'l'addition (a+b = b+a, le nombre 0 est l'élément neutre pour l'addition) etc
Mais la puissance de la notion de groupe est reliée a une notion centrale dans un certain nombre de science, la notion de symétrie. C'est ainsi qu'on défini un "groupe de symétrie" c'est a dire une série de transformation géométrique qui laissent l'objet à étudier invariant. Une de ces transformation les plus connues sont les "groupes de Lie"trés utilisés en physique fondamentale.
Pour approfondir ce sujet, je vous propose la série de vidéo youtube réalisées par Mickaël Launay qui est un mathématicien et vidéaste de talent, auteur d'une série d'ouvrages dont le dernier est tout a fait passionnant Le théorème du parapluie ou l'art d'observer le monde dans le bon sens mais aussi d'un blog et d'une chaîne YouTube très courue...
Il a réalisé sur sa chaîne youtube toute une série de vidéos pédagogiques faciles d'accès sur les structures algébriques dont cette théorie est le pivot central. Je vous en ai sélectionné deux d'entre elles.
Pour accéder à l'ensemble des vidéos : cliquez ici
Les deux vidéo sélectionnées :
Simuler la propagation des virus
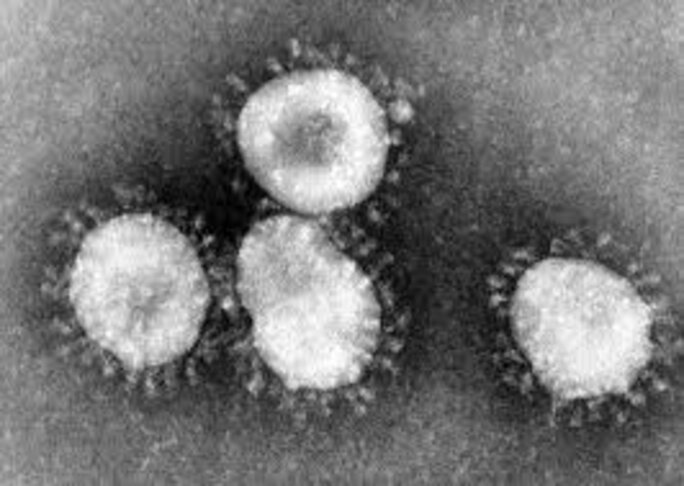
L'actualité des problèmes de santé font qu'on parle beaucoup de l'épidémie de Coronavirus en Chine Les avis les plus divers circulent : certainEs parlent d'un "prétexte" (étant donné le peu de cas de malades affectés jusqu'a présent) pour "parler d'autre chose", d'autres utilisent la théorie du complot (la maladie serait l'invention de forces forcément occultes) sans compter toutes celles et ceux qui présentent les conséquences potentiellement catastrophique de cette nouvelle épidémie avec certitude.
Mais le mieux est de se fier aux résultats de la science, qui nous permet de mieux modéliser le développement de la maladie en fonction de différents paramètres comme la mortalité potentielle, le taux de contamination et le taux de propagations L'épidémiologie est cette nouvelle discipline scientifique qui utilise les mathématiques et la biologie pour comprendre les mécanisme de propagation et de réplication des épidémie, afin d'en comprendre les mécanismes, de pouvoir prévoir leurs conséquences et d'adapter le dispositif médical en conséquence.
Les mathématiciens modélisent les épidémies, ce qui permet de calculer leur évolution. Ces calculs aident à prévoir des mesures de santé publique adaptées. Mais ils sont aussi l'objet d'interprétations cavalières et la source d'affirmations exagérément précises telles que « le pic de l'épidémie de grippe aura lieu la semaine prochaine ».
Les mathématiques utilisent la "théorie des graphes" pour répondre à ce type de question avec une bonne efficacité, d'autant que les performance de calcul actuelle sont sans commune mesure avec les résultats qu'on pouvait espérer il y a peu. La simplicité du modèle permet de mener tous les calculs à bien. Les humains sont alors les sommets du graphe et ils sont reliés par une arête s'il y a une possibilité de transmission entre deux individus. Le graphe associé à une école maternelle est complet au sens où tout élève peut rencontrer tous les autres élèves dans la cour de récréation, donc chaque sommet est relié à tous les autres. En revanche, pour une population rurale isolée, on peut imaginer un graphe « étoilé » où un sommet - par exemple le facteur - est rattaché à tous les autres, lesquels ne sont pas reliés entre eux.
Comment s'opère la propagation ? Dans ce modèle, on commence par choisir au hasard un sommet du graphe que l'on déclare infecté : c'est le foyer de l'épidémie. Puis on choisit au hasard l'un de ses voisins et on décide que ce voisin est désormais contaminé (même s'il l'était déjà). On se demande alors combien d'étapes il faut pour contaminer toute la population. Le cas où un certain groupe de sommets serait isolé (une mise en quarantaine, par exemple) est éliminé, puis on effectue calculs et simulations. Le résultat dépendra de la façon dont sont choisis les sommets à chaque étape : chaque simulation sera a priori différente (à cause du hasard), de sorte que le résultat est une variable aléatoire. Les propriétés des résultats (en termes mathématiques, la loi de la variable) dépendent de la forme du graphe, de sa « géométrie ».
Pour en savoir plus : Nous modélisons la propagation des virus La recherche "Les maths et le réel : comment modéliser le monde Numéro spécial septembre novembre 2019.
du coté des revues
La france est le pays des revues de vulgarisations scientifique. Ce mois-ci nous présenterons une revue d'histoire naturelle assez remarquable, la revue "Espéces" une revue universitaire diffusée en kiosque; C'est une revue de vulgarisation de haute tenue, aux articles passionnants

Dans la dernière livraison, il y a en particulier tout un dossier sur les "espèces envahissantes" tout à fait remarquable ! Voila comment la directrice de publication présente sa revue : "Nous sommes une sorte d’intermédaire entre la presse scientifique en kiosque, qui doit traiter un grand nombre de sujets dans un espace restreint, la presse écologiste (nous ne sommes pas une presse d’opinion, nous tentons de donner un l’information la plus objective possible pour que le lecteur puisse s’en forger une), et les publications scientifiques. Les articles sont longs, détaillés, en majorité directement écrits par les scientifiques, nous nous sommes dotés d’un conseil scientifique qui relit les articles. Espèces est aussi largement illustrée, vulgarisée, variée dans ses sujets et bourrée d’infos et d’actualités... et nous y ajoutons un peu d’humour " Bref, une revue dont je ne peut plus me passer, et facilement disponible, en kiosqie ou en bibliothéque.
Le scientifique du mois Sophie Germain

Agrandissement : Illustration 6

Sophie Germain est une des premières femmes mathématiciennes. Brillante autodidacte, estimée par quelques uns de ses pairs, elle s'est toutefois heurtée à l'intransigeance de son époque envers les femmes savantes.
Elle nait à l'époque ou les femmes sont censées s'occuper de leurs famille, et pas de découvertes scientifiques ou de mathématiques. Très tôt, elle se découvre une passion pour les sciences. Le moins que l'on puisse dire est que ses parents n'encouragent pas cette vocation. Elle luttera pourtant avec acharnement pour se cultiver, ses connaissances de base étant par obligation autodidacte. On dit même qu'elle se levait la nuit pendant le sommeil de ses parents pour aller étudier à la lueur d'une bougie.
À19 ans, elle parvient à obtenir les notes de cours de l'Ecole Polytechnique nouvellement créée. Elle commence à entretenir une correspondance avec Lagrange, qui y est professeur d'Analyse, sous le pseudonyme de "Mr Le Blanc". Lorsque Lagrange découvre la supercherie, il est profondément admiratif devant le courage de cette femme.
La théorie des nombres est le premier domaine où Sophie Germain apporte une contribution importante. Elle est d'ailleurs encore connue pour ses recherches dans ce domaine À la suite de la visite du physicien allemand Chladni à Paris en 1809, Sophie Germain change radicalement d'orientation mathématique. Pendant plus d'une décennie, elle s'intéressera à la théorie des surfaces (principalement à leur courbure) et au problème de vibration des surfaces élastiques. Elle présente plusieurs mémoires à l'Académie des Sciences, et s'oppose violemment à Poisson sur ces sujets. En 1816, elle est la première femme à remporter un prix de l'Académie, puis à assister à ses séances sur son seul mérite. Devenue amie de Fourier, lui-même secrétaire perpétuel de l'Académie depuis 1822, Sophie Germain continue à travailler jusqu'à la fin de sa vie sur les mathématiques et la philosophie.
La découverte du mois : trace de pieds néanderthaliens en Normandie

Agrandissement : Illustration 7

Avant les centaines d'empreintes trouvées au Rozel, nous n'avions à l'échelle de l'Europe que quelques traces de pieds néandertaliens, à savoir 1 empreinte mal conservée datée de quelque 236000 ans à Biache-Saint-Vaast en France, 3 empreintes datées de quelque 130000 ans dans la grotte de Theopetra en Grèce, 3 empreintes datées en 62000 et 97000 ans dans la grotte Ghețarul de la Vârtop en Roumanie et finalement dans la paléodune de Catalan Bay à Gibraltar une empreinte curieusement datée d'il y a 28000 ans. Plus rares encore sont les empreintes de main trouvées au Rozel, dont une montre de façon particulièrement distincte toutes les empreintes des doigts, dont un pouce particulièrement large typique des néandertaliens.
Le livre du mois : Carlo Rovelli Ecrits vagabonds

Agrandissement : Illustration 8

Ecrire un ouvrage de vulgarisation scientifique est susceptible de multiples approches Celle du journaliste qui use de ses outils professionnels (recherche de l'information, confrontation des sources) est très différente de celle du scientifique qui est lui même à l'origine de la découverte qu'il ou elle nous présente. Et le scientifique lui même met beaucoup de lui même dans son ouvrage,
Carlo Rovelli est un des scientifiques les plus avancés dans la résolution d'un des problèmes les plus fondamentaux de la physique actuelle, le fait de concilier les deux théories fondamentales qui organisent l'univers théorique de la physique : la mécanique quantique et la relativité généralisée. Il défend une approche originale qu'il a présentée dans plusieurs ouvrages, la gravitation quantique à boucle. Mais il est connu également pour s'intéresser à la philosophie (une de ses originalités est de penser que les difficultés a dépasser les théories de physique fondamentale des précurseurs du XX siècle est le manque de culture philosophique des scientifiques actuels) mais aussi a s'intéresser de façon approfondie a l'histoire de sa discipline (l'ouvrage qu'il a consacré à Anaximandre de Milet est assez remarquable)
L'ouvrage qu'il nous propose aujourd'hui est original dans ce sens qu'il n'est pas comme ses autres ouvrages un approfondissement autour d'un thème précis, mais un ouvrage "à saut et à gambade" comme le précise l'expression de Montaigne dans ses essais ou il précise : " J'aime l'allure poétique, à sauts et à gambades. C'est un art, comme dit Platon , léger, volage, démoniaque. Il est des ouvrages en Plutarque où il oublie son thème, où le propos de son argument ne se trouve que par incident, tout étouffé en matière étrangère : voyez ses allures au Démon de Socrate"
Bref, voila une suite de courtes notations publiées dans de courtes chroniques pré-publiées dans une série de journaux italiens (le Corriere della Sera ou il sole 24 ores, (un équivalent des "echos" transalpin) C'est frais, bondissant, délicieux. Cela parle de science (les trous noirs, la conception du temps dans la physique fondamentale, les erreurs d'Einstein) mais aussi de philosophie, d'éthique, de politique. Et cela montre une conception essentielle de l'auteur, la générosité. Et c'est un plaisir de lecture sans pareil. Chaudement recommandé !
Présentation de l'éditeur:
Esprit libre, scientifique de renom, curieux de philosophie et d’humanités, Carlo Rovelli est aussi un formidable conteur. Sa curiosité l’amène à s’interroger sur le monde qui nous entoure, sur la nature du temps qui passe, et jusqu’aux grandes questions philosophiques aux réponses incertaines.
Il rassemble ses réflexions dans ces Écrits vagabonds, un recueil de textes accessibles, composés au long cours, qui va des trous noirs à la Lolita de Nabokov, du LSD au plaisir de voyager en Afrique, de l’athéisme à l’alchimie de Newton, de la philosophie analytique aux erreurs d’Einstein.
Dans ce journal de bord d’une intelligence toujours en mouvement, le lecteur fera l’expérience d’une pensée qui s’intéresse à tout, subtile, profondément contemporaine. Il rencontrera un esprit en quête continuelle d’une cohérence où science, littérature et philosophie dialoguent harmonieusement.
Un précipité de connaissance et d’inventivité.
Tout un homme, fait de tous les hommes et qui les vaut tous et que vaut n'importe qui
Les jeux
Ce mois ci, pour féter le retour de cette rubrique, des jeux "spécial brexit" spécialement concoctés pour vous. Il y sera beaucoup question de statistique. Rappelons la citation de Mark Twain : il y a trois sorte de mensonges : les mensonges, les sacrés mensonges et les statistiques.

Politique britannique
Nous somme la veille du vote solennel pour l’adoption finale du Brexit par le parlement britannique. Celui ci compte 634 membres dont 338 conservateurs 256 travaillistes 14 socio démovrates 5 autonomistes gallois ou écossais 10 unionistes de l’Ulster
Pendant la séance solonelle décidant de l'adoption définitive du brexit, on compte autant de travaillistes présents que de conservateurs absents autant unionistes irlandais absent autonomistes présents et autant de libéraux présents que de socio démocrates absents
Quelle est la probabilité que le très honorable Bryan Smith député du compté de North Somborne soit présent au parlement lors de ce vote décisif ?
Statistique écossaise
Le North British Demographic Institut est une fort recommandable institution britannique des statistiques. Voilà un sondage qu'elle a réalisé dans la ville d'Edimbourg, la future capitale de l'Ecosse indépendante auprès de 1000 habitants représentatifs de la population globale.
Elle a trouvé 500 hommes et 500 femmes, 781 personnes portent un pantalon et 412 un chapeau, dont 159 femmes. De même compte-t-on 323 femmes en pantalon. De plus, 298 personnes portent pantalon et chapeau, dont 68 femmes
combien compte-t-on d'hommes en kilt ?
La météo sur le channel
Pour prévoir la météorologie sur la manche, la météo française se trombe une fois sur 5 et la météorologie britannique une fois sur 7. France météo prévoit un temps dégagé, et le Met Office un brouillard a découper au couteau. Quelle est la probabilité d'avoir "the fog in the channel" ?
Je remercie celles et ceux qui m'ont fait remarquer une erreur ou contester une affirmation...



