L’invention du calcul en Inde

Blog Labyrinthe des sciences et des arts

Le chapitre 3 de Cultural Foundations of Mathematics: the Nature of Mathematical Proof and the Transmission of the Calculus from India to Europe in the 16 c. EC (C. K. Raju, 2007, p. 109-200) est une analyse détaillée, techniquement étayée et documentée, du développement des mathématiques indiennes à partir des travaux d'Āryabhaṭa au 5^e siècle EC.

Auteur de la plus ancienne méthode de calcul des racines carrées, Āryabhaṭa a principalement contribué au passage de l'approche ancienne géométrique à celle du calcul pour la mesure de longueurs, aires et volumes de lignes et surfaces courbes. En ne citant que Nīlakanṭha (16^e siècle), les historiens — et les nationalistes hindous ! — ont tendance à réduire la lignée des mathématiciens à l'emblématique « École du Kerala » qui passe sous silence les contributions de mathématiciens originaires d'autres régions (ou d'autres pays), soigneusement répertoriées et mises en perspective dans ce chapitre.

C. K. Raju décrit les étapes de recherche qui avaient pour objet de (1) trouver des séries à convergence rapide, (2) minimiser le temps de calcul, (3) augmenter la précision des résultats grâce à un facteur correctif (saṃskāra, page 174) et l'interpolation linéaire (p. 138) ou quadratique (p. 140), enfin et surtout (4) déterminer le nombre d'itérations nécessaires en fonction de la précision souhaitée.

Les détails complets, présentés ici pour la première fois, démontrent qu'il existait une preuve (pramāṇa) valide des séries infinies indiennes, contrairement à Newton, etc. qui n'ont pu fournir à leurs contemporains aucune preuve ni dérivation claire de ces mêmes séries infinies. De plus, contrairement à l'apparition subite des séries infinies en Europe, au 17^e siècle, les séries infinies indiennes ont évolué sur une période de mille ans, tandis que la précision des calculs trigonométriques était poussée de la première minute (Āryabhaṭa 5^e s. EC) à la deuxième minute (Vaṭeśvara 9^e s. EC) et enfin à la troisième minute — tentée par exemple par Govindasvāmin (9^e s. EC) et réalisée par Mādhava (14^e-15^e s. EC).

Āryabhaṭa a utilisé une technique élégante de différences finies et de quadrature numérique, contrepartie numérique du théorème fondamental du calcul. L'utilisation des différences secondes pour l'interpolation quadratique a ensuite été étendue aux ordres supérieurs, faisant appel à l'expansion en série de fractions. Par analogie avec les séries numériques, les développements de fractions continues ont été utilisés pour représenter une série infinie de fonctions rationnelles.

Tous ces travaux des mathématiciens indiens répondaient au besoin d'appliquer le calcul aux observations astronomiques, permettant une mesure rigoureuse de la latitude pour la navigation — bien plus précise qu'avec les cartes des Européens à cette époque — et établissant un calendrier avec une position correcte des équinoxes (pour la mesure diurne des latitudes, etc.). Tout cela en l'absence de machines à calculer !

C'est cette approche épistémologique, indissociable de son histoire, qui caractérise les mathématiques indiennes — voir la conclusion aux pages 184-185.

Exemple : méthode des différences finies en trigonométrie

Page 130 est présentée une « table » publiée sous cette forme dans le Gaṇita d'Āryabhaṭa (verset 12):

À première vue, on pourrait penser à un poème sanskrit rendu facile à mémoriser par la répétition de syllabes : maki, bhaki, phaki, etc. Sauf que son contenu n'a rien de poétique ! C'est la table de sinus d'Āryabhaṭa. Son décodage fait appel à une table de conversion exposée au début du Gaṇita. Les combinaisons de consonnes et voyelles permettent de construire des nombres en notation décimale (explication pages 130-131).

Selon cette convention, le verset 12 se traduit simplement :

225 224 222 219 215 210 205 199 191 183 174 164 154 143 131 119 106 93 79 65 51 37 22 7

Ces nombres sont les différences successives entre les valeurs de R.sin(n.β) pour n de 1 à 24 et β = 1/24^e de quadrant de cercle = 225 minutes d'arc. Le périmètre du cercle trigonométrique est aussi exprimé en minutes d'arc, soit 360 x 60 = 21600' correspondant à un rayon de 3438. Par exemple, pour calculer le sinus de 10 x 225' = 2250' = 37° 30', il suffit d'additionner 225 + 224 + 222 + … + 183 = 2093 puis de diviser par 3438 ce qui donne 0.60878 ≈ sin(2250/60).

(La division par le rayon du cercle n'est donnée qu'à titre de vérification sur une calculette. Les géomètres indiens travaillaient directement avec les longueurs d'arc — grandeurs dont le calcul, selon Descartes, échappait à l'esprit humain puisque π ne pouvait pas être calculé exactement…)

➡ Remarquez au passage les 5^e, 6^e et 7^e nombres :  णखि, ञखि, ङखि qui se prononcent ṇakhi, ñakhi et ṅakhi respectivement… Seuls les autochtones ayant une parfaite articulation (et une oreille familière des phonèmes devanagari) éviteront un naufrage en confondant les valeurs 215, 210 et 205 !

Āryabhaṭa explique plus loin sa méthode de calcul des différences finies (voir pages 132-135) affinée aux 15^e et 16^e siècles par Nīlakaṇṭha Somayāji qui a poussé la précision du calcul à la seconde près. C'est ce savoir qui a été traduit et exporté vers l'Europe par les Jésuites portugais.

En visite à Cochin, peu de temps avant la réforme du calendrier grégorien par Clavius, Matteo Ricci écrit qu'il cherche « un brahmane intelligent ou un honnête Maure » pour lui expliquer les méthodes indiennes de mesure du temps (L'Occident a-t-il inventé la science ? page 66, voir source).

On comprend ainsi pourquoi le modèle planétaire de Tycho Brahe était identique à celui de Nīlakaṇṭha. Les instruments de mesure de Brahe étaient bien trop imprécis, et construits bien trop tard, pour qu'il soit parvenu à son modèle de manière indépendante (ibid. page 67).

La navigation

Les tables et techniques de calcul, documentées dès le 5^e siècle, servaient à la fois aux calculs de calendrier et à la navigation. L'utilisation de représentations textuelles n'avait rien d'ésotérique puisque les règles de décodage étaient énoncées au début des traités. Il s'agissait en fait d'un moyen mnémotechnique utilisé par les navigateurs.

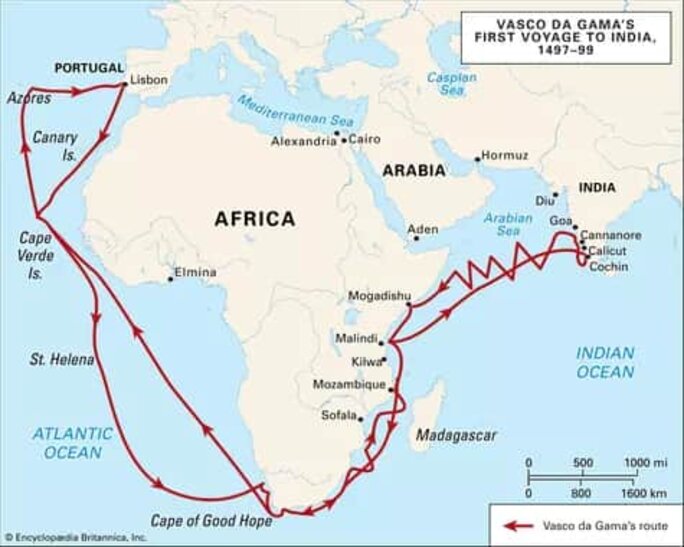
Cette manière de procéder n'était pas l'exclusivité des Indiens car leurs partenaires commerciaux chinois, africains et arabes utilisaient des méthodes semblables à une époque où les navigateurs européens — comme Vasco de Gama qui découvrit les Indes (!) en 1497 — devaient se contenter de sillonner les côtes faute de cartes précises et d'instruments de navigation. C'est un pilote indien (ou arabe) qui a conduit Vasco de Gama de Melinde (Afrique) à Kozhikode (Calicut) sur la côte du Malabar (page 240).

Utilisé par les navigateurs dans le Lakshadweep, le kamāl était depuis longue date un instrument permettant de déterminer la latitude avec une précision proche de 10 minutes d'arc, grâce à un mécanisme de double graduation apparenté au vernier (voir pages 247-251).

Une telle mesure exigeait des tables trigonométriques plus précises que celles d'Āryabhaṭa (5^e siècle) et de Brahmagupta (7^e siècle), comme celle de Vaṭeśvara (904 EC) qui calculait sur 56 minutes 15 secondes d'arc et proposait une procédure d'interpolation quadratique (page 252).

La précision du calcul de latitude permettait de passer assez près d'une une île pour la repérer à vue en se déplaçant sur le parallèle calculé.

➡ Dans son roman Boussole (Actes Sud, 2015 page 112), Mathias Enard évoque les poèmes que les marins arabes employaient autrefois comme aide-mémoire pour la navigation.

Autres lectures recommandées :

• C. K. Raju, L'Occident a-t-il inventé la science ? Paris : Hic Sunt Dragones, 2022. Trad. B. Bel
  https://hicsuntdracones.fr/loccident-a-t-il-invente-la-science/
  https://www.amazon.fr/LOccident-inventé-Science-C-K-Raju/dp/249005063X
• C. K. Raju, En finir avec « Euclide » : le discours sur la supériorité raciale et civilisationnelle :
  https://hicsuntdracones.fr/en-finir-avec-euclide-le-discours-sur-la-superiorite-raciale-et-civilisationnelle/
• Agathe Keller, Un commentaire indien du VII^e siècle, Bhâskara et le ganitapada de l’aryabhatiya. Thèse de doctorat. Université Paris 7, 2005. https://halshs.archives-ouvertes.fr/halshs-00006349
• C. K. Raju, The Eleven Pictures of Time: The Physics, Philosophy and Politics of Time Beliefs. Sage, 2003.
• C. K. Raju, Time: Towards a Consistent Theory. Dordrecht : Kluwer, 1994.

C. K. Raju est mathématicien et physicien. Auteur de plusieurs ouvrages, dont deux autres sont à paraître aux éditions Hic sunt dracones, il propose un enseignement « décolonialisé » des mathématiques, de la physique, de l’histoire et de la philosophie des sciences.