Blog Labyrinthe des sciences et des arts
Note musicale
Extrait de C. K. Raju, L'Occident a-t-il inventé la science ?. Paris : Hic Sunt Dracones, 2022, p. lxxxi-lxxxiv.
Détaché en Inde par le CNRS au printemps 1994, j’étais invité au Centre for Development of Advanced Computing (C-DAC) de Pune pour un exposé sur la représentation du temps en informatique musicale.

La maison d’hôtes du C-DAC étant presque inoccupée, j’ai lié conversation avec le seul résident présent au salon du petit-déjeuner. Nous avons échangé sur les raisons de notre séjour à Pune. Mon interlocuteur était chargé de l’implémentation de logiciels dans le superordinateur PARAM construit au C-DAC – deuxième ordinateur le plus puissant au monde après ceux des USA.
L’acronyme PARAM (en sanskrit « suprême ») signifie « PARAllel Machine ». Le mathématicien et informaticien C. K. Raju avait été engagé pour son expertise sur le parallélisme, en lien avec son approche novatrice de la modélisation du temps en physique théorique. Notre dialogue a mis au jour une passion partagée pour le refus de réduire le temps à un objet « métaphysique » d’une stricte linéarité – celui des séquenceurs et boîtes à rythmes en musique…
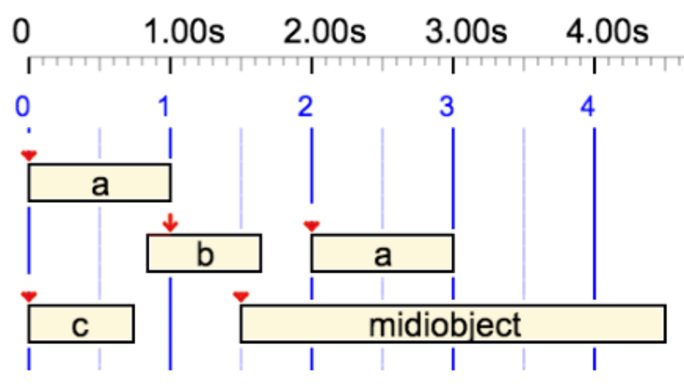
J’avais conçu un modèle polymétrique qui permet au compositeur de manipuler une description incomplète des structures d’objets sonores, ces objets étant libres de se positionner en respectant des contraintes métriques et topologiques. Au niveau supérieur, la structure temporelle de l'œuvre musicale est produite par un mécanisme d'inférence qui n'est pas toujours réversible.
La théorie de C. K. Raju m’intriguait par de nombreux aspects auxquels je n'avais qu'un accès superficiel en lisant des articles pour non-spécialistes. Son hypothèse de « boucles temporelles » avait aussi inspiré ma compagne Andréine dans sa création chorégraphique Cronos.
Nous avons à plusieurs reprises renoué contact avec C. K. Raju, jusqu’à notre retour en France en 1998. Par la suite, j’ai lu The Eleven Pictures of Time (2003) et tenté de déchiffrer Time: Towards a Consistent Theory (1994).

Agrandissement : Illustration 3

Mais c’est l'ouvrage monumental Cultural Foundations of Mathematics (Pearson Longman 2007, 477 pages) qui m’a ouvert les yeux sur son travail d’historien des mathématiques et des sciences physiques. J’ai commencé à comprendre les fondements du calcul (ganita) selon la tradition indienne.
La musique et les mathématiques ont en commun l'affirmation de leur « universalité » par delà les cultures, un privilège hérité de la vision de l'Occident comme aboutissement de toutes les branches du savoir humain. En explorant la complexité des musiques « extra-européennes », les (ethno)musicologues du 20e siècle ont certes remisé cette prétention de supériorité du système tonal européen, mais sans pour autant renoncer à une démarche « comparative » (ethnocentrique). Le travail de « décolonisation » amorcé en musicologie fait encore plus cruellement défaut pour ce qui concerne les mathématiques.
Mes travaux sur le temps musical avaient pris racine dans une modélisation informatique des schémas d’improvisation des percussionnistes indiens, affranchie des conventions de la notation musicale en Europe. Travaillant par ailleurs sur l’intonation microtonale du raga, j'ai approfondi la lecture de textes anciens décrivant les intervalles musicaux.

Agrandissement : Illustration 4

L’expérience des deux vinas (chapitre 28 du Nāṭyaśāstra) est exemplaire de la manière dont les philosophes et mathématiciens indiens utilisaient la preuve empirique (pratyakṣa) comme validation (pramāņa) des connaissances, là où les Occidentaux exigent des preuves formelles déduites de postulats.
Comme le rappelle Raju dans ce livre, toute preuve scientifique nécessite un détour par la réalité : la vérification empirique du modèle théorique.
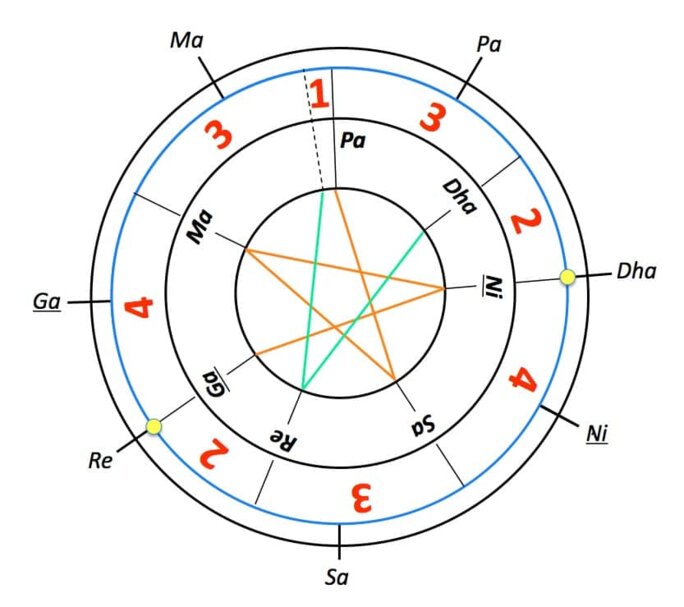
Agrandissement : Illustration 5

Ainsi, pour les théoriciens de la musique en Inde, le concept de tonalité n’était pas déduit d’idées préconçues sur des longueurs de cordes vibrantes ni des rapports numériques de fréquences. La gamme fondamentale indienne (grāma) était décrite par une expérience de pensée dont l'étape initiale consistait à construire le plus petit intervalle tonal significatif (pramāņa ṣruti) sur la base de sa perception sensorielle : « […] lorsque le relâchement ou la tension des cordes se produit ».
Traduit en équations, ce modèle tonal se prête à des généralisations qui tiennent compte de l’étirement des octaves ou de l’inharmonicité des sons partiels. Il permet surtout de programmer (et de comparer) les systèmes de tempérament pratiqués en Europe, matérialisés – là aussi de manière empirique – par les accordeurs d’instruments.
C. K. Raju est allé bien au delà de la relecture des textes mathématiques anciens.

Agrandissement : Illustration 6

Il a développé cette approche du calcul pour construire des outils conceptuels applicables à la résolution de problèmes difficiles de physique théorique, sans oublier l'enseignement des mathématiques « normales » à de jeunes étudiants.
C’est ce travail inestimable que je m’efforce aujourd’hui de mettre à disposition du lectorat francophone. Et je tiens à remercier Daliborka Milovanovic pour son aide précieuse à l'édition critique et la mise en forme de la traduction.
Bernard Bel
Traducteur de L'Occident a-t-il inventé la science ? et Euclide, le sabre et le goupillon.



