Blog Labyrinthe des sciences et des arts
Le juriste Alain Supiot a donné au Collège de France, en 2012 et 2013, une excellente série de cours exposant sa thèse : « Du gouvernement par les lois à la gouvernance par les nombres ». Nous sommes gouvernés par les nombres, c'est un phénomène enclenché il y a longtemps et devenu explicite dans les algorithmes et le Big Data machine-learning stupidement rebaptisé « intelligence artificielle » — voir Le Théorème d'hypocrite. Mais on peut dire que cette approche a été renforcée, légitimée, instrumentalisée par la doctrine chrétienne qui sacralisait les nombres, les mathématiques étant le langage de Dieu et donc supposément de la perfection — voir Euclide et Jésus.
C'est cette mystique des nombres qui crée de la confusion dans toutes les théories de la musique, en Europe mais aussi dans les pays colonisés par l'Europe.
Quand je suis arrivé en Inde pour étudier expérimentalement le système tonal (shruti-grama-murchhana), j'avais la tête remplie des idées issues du modèle d'Helmholtz : les intervalles corrects ne pouvaient être que des fractions entières simples comme 3/2, 5/4, 8/5, 15/8 etc.

Agrandissement : Illustration 1

Cette conviction était aussi celle de mon partenaire Jim Arnold qui avait étudié les textes anciens en s'appuyant sur les interprétations de musicologues indiens eux-mêmes « colonisés » par le modèle occidental. On pouvait effectivement expliquer la division de l'octave en 22 intervalles inégaux en attribuant à chaque position une fraction assez simple. Le philosophe français Alain Daniélou, influencé par sa culture franc-maçonne (prétendument pythagoricienne) sur la magie des nombres entiers, avait étendu ce système pour diviser l'octave en 52 positions, ce qui d'après lui corroborait certains écrits théoriques indiens.
Pour vérifier ces théories, j'avais construit un Shruti Harmonium rendant possible de programmer finement n'importe quelle position tonale (précision meilleure que 1 centième de demi-ton). La même année, Daniélou avait fait construire un instrument similiaire, appelé S-52, par l'entreprise suisse Kudelslki qui à cette époque fabriquait les célèbres magnétophones Nagra. Mais le S-52 n'était pas accordable, car Daniélou était persuadé de l'unicité et de la perfection de son modèle.

J'ai assisté à la présentation publique du S-52 à Paris, en 1980, où le maître essayait de jouer au clavier des phrases musicales de ragas en utilisant les intervalles « parfaits » selon ses prédictions. C'était atroce à entendre. Les gens se retenaient de rire car Daniélou était par ailleurs un personnage charmant (et généreux).
Après cette démonstration, j'ai eu une discussion en aparté avec Stefan Kudelski qui m'a lancé avec son bel accent suisse : « Cet instrument est appelé le “sauve-qui-peut” dans notre atelier, car personne ne saura jamais en jouer et personne n'aimerait la musique qu'il pourrait produire ! »
Je suis revenu en Inde à cette époque (1980) avec le Shruti Harmonium qui permettait d'ajuster (sur un clavier numérique) les intervalles selon les instructions de musiciens experts, comme le joueur de rudra vina Asad Ali Khan ou la chanteuse Kishori Amonkar.

Agrandissement : Illustration 3

Mais nous avons vite découvert que (1) les intervalles prévus par notre interprétation occidentale du système shruti-grama-murcchana n'étaient pas reconnus par ces musiciens, et (2) il s'avérait impossible de leur demander d'accorder un instrument à tons fixes sur les positions tonales qu'ils imaginaient correctes dans les ragas.
C'est alors que nous avons changé de dispositif expérimental en construisant le premier Melodic Movement Analyser (MMA), lui aussi avec une précision meilleure que le cent (soit 1 pour mille de la fréquence). En amont, j’avais aussi conçu un extracteur de fréquence fondamentale exploitant une batterie de filtres tiers d’octave. Changement de méthodologie : on examinait les faits, ce que faisaient rarement les musicologues, au lieu de les embarquer dans un modèle axiomatique.

Agrandissement : Illustration 4

Le MMA nous a permis de visualiser avec précision les mouvements mélodiques. Mais je l'avais surtout conçu pour l'analyse : par un traitement statistique (selective tonagrams) on pouvait extraire le squelette tonal de l'interprétation d'un raga. Là aussi nous avons constaté que ces mesures ne validaient pas le modèle simple : des rapports de fréquences comme 81/64 (tierce majeure pythagoricienne) n'étaient jamais utilisés, par contre on voyait apparaître des positions intermédiaires, par exemple à mi-chemin entre 81/64 et 5/4 (tierce majeure harmonique). Était-ce un simple ajustement ou l'indication d'un modèle théorique plus complexe ?

Agrandissement : Illustration 5

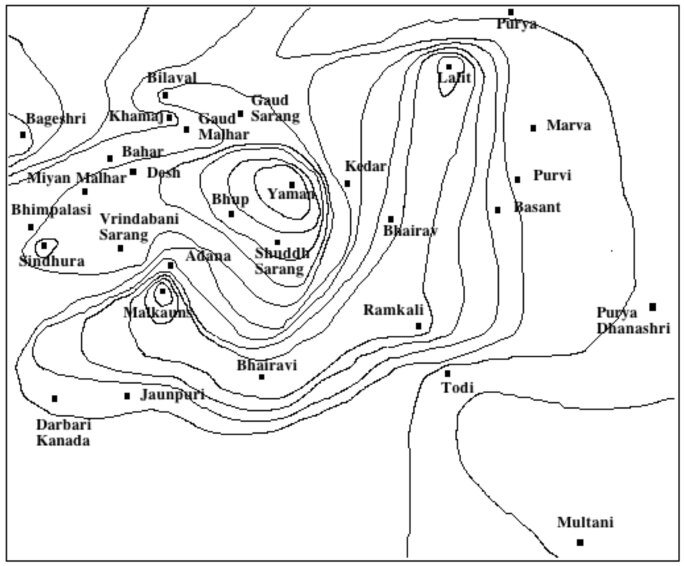
Agrandissement : Illustration 6
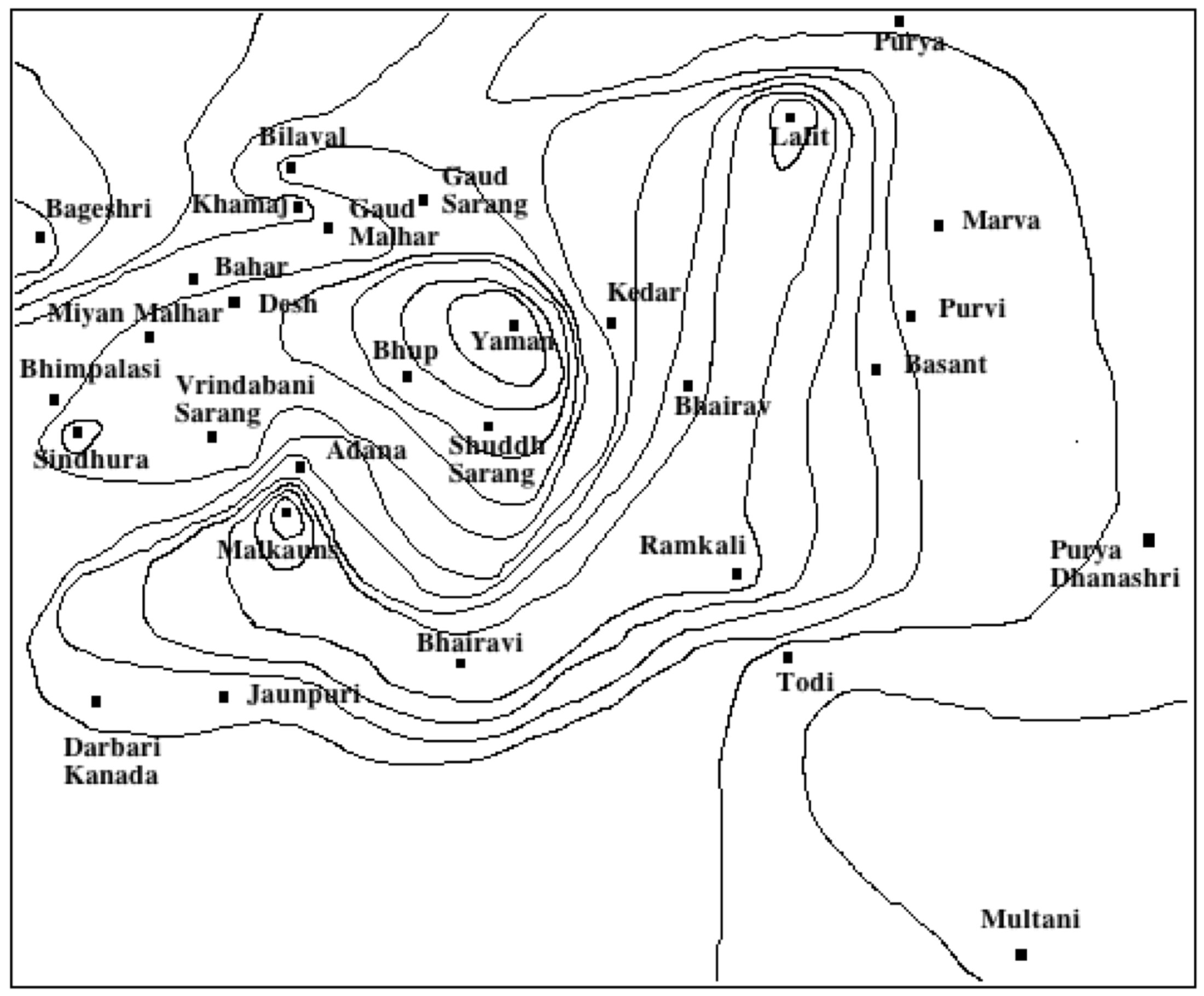
Mes collègues hollandais (Wim van der Meer) et indiens (Suvarnalata Rao) n'ont pas poursuivi cette recherche théorique car ils étaient plus intéressés par la visualisation des mouvements mélodiques, dans une démarche documentaire et pédagogique qu'ils ont menée à bien avec de nouvelles technologies — le projet AUTRIM (https://autrimncpa.wordpress.com/).
De mon côté, j'ai relu les travaux de Jim Arnold qui s'était intéressé au plus ancien texte indien sur le système tonal : le chapitre 28.24 du Natya Shastra. J'étais très étonné que l'auteur (les auteurs ?) de ce traité n'ai(en)t utilisé aucun nombre pour décrire les intervalles. C'est encore plus surprenant quand on sait qu'à cette époque les bases du calcul étaient plus que suffisantes, en Inde, pour construire un modèle aussi élaboré que celui attribué à « Pythagore » en Occident.
L'auteur du Natya Shastra aurait pu, par exemple, spéculer (comme, des siècles plus tard, Jean-Philippe Rameau) sur les rapports de longueurs de cordes vibrantes et retrouver ainsi les fractions magiques 2/1, 3/2, 5/4, 15/8 etc. Rien de tout cela ! Dans l'expérience des deux vinas, le plus petit intervalle tonal significatif (pramāņa śruti) est défini à partir d'une expérience perceptive : “The difference which occurs in Pañcama when it is raised or lowered by a Śruti and when consequential slackness or tenseness [of strings] occurs, will indicate a typical (pramāņa) Śruti” — ce qui revient à dire : « […] lorsque le relâchement ou la tension des cordes se produit ». D'après la procédure ainsi décrite, cet intervalle est aussi celui entre les tierces majeure harmonique et pythagoricienne.
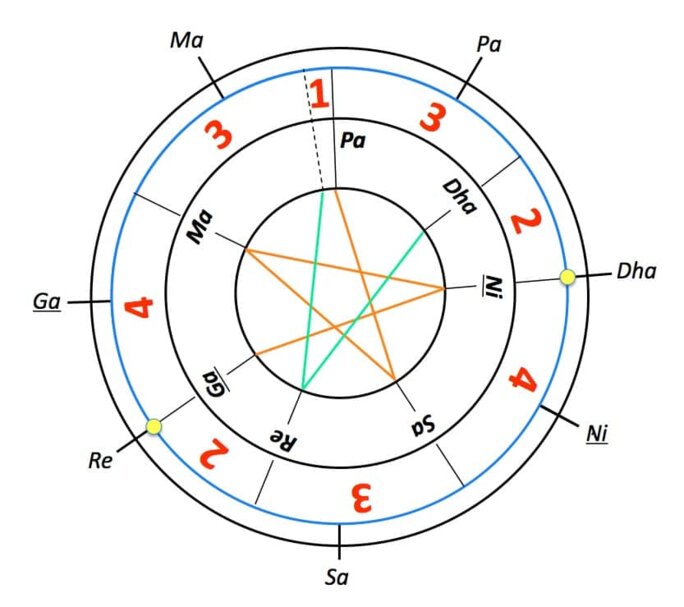
Agrandissement : Illustration 7

Pour cette raison, les musicologues occidentaux et indiens (ces derniers influencés par les Occidentaux) en ont déduit que ce pramāņa śruti ne pouvait être qu'un rapport de fréquences 81/80, faisant ainsi coincider le modèle indien antique avec celui théorisé en Europe, ce qui revenait à valider le modèle indien selon le standard des « civilisés »… La validation par un homme blanc dont C. K. Raju parle souvent !
Mais quelque chose ne va pas bien dans ce raisonnement : l'intervalle de la tierce majeure harmonique (7 śruti) est désigné comme assonant (anuvadi) dans la théorie indienne ancienne. De la même manière, la tierce majeure a été longtemps interdite par l'Église en Europe, car dissonante et non conforme à l'idée de la perfection divine, cette interdiction ayant pris fin au Concile de Trente (1545-1563).
Agrandissement : Illustration 8
Si le pramāņa śruti n'a pas une taille définie, il manque trois équations au système qui permettrait de quantifier les 22 positions tonales (voir mon article). Deux équations seraient celles définissant l'octave (environ 2/1) et la quinte (environ 3/2), la troisième étant celle précisant le pramāņa śruti ou, de manière équivalente, la tierce harmonique.
Le modèle décrit dans le Natya Shastra est donc un modèle flexible, ce qui explique qu'il ne peut pas être réduit à un tableau de fractions entières. Toutefois, bien sûr, il peut être implémenté dans des algorithmes, ce que j'ai fait pour étudier plus en détail l'intonation des ragas (https://bolprocessor.org/raga-intonation/).
La démonstration est peut-être convaincante mais incomplète : que faisaient les accordeurs d'instruments en Europe avant le Traité de l'harmonie réduite à ses principes naturels (Rameau en 1722) et les Causes physiologiques de l'harmonie musicale (Helmholtz en 1877) ? La réponse est simple : ils se fiaient à leur oreille ! Exception faite, peut-être, du mathématicien Joseph Sauveur, qui était quasiment sourd et a malgré cela conçu un tempérament mésotonique très apprécié (voir https://bolprocessor.org/tonal-analysis/).
C'est parce qu'il n'existait pas de théorie numérique des intervalles à cette époque que l'on déconsidère aujourd'hui la pratique du tempérament comme empirique (approximative) et donc (la pire injure) pré-scientifique.
Agrandissement : Illustration 9
Pour cerner la réalité, il faut étudier sans préjugé les documents historiques de cette époque. C'est ce qu'a fait Pierre-Yves Asselin, que Jim et moi avions rencontré à Paris pendant son travail de thèse en 1979.
Cette thèse a été soutenue au laboratoire d'Émile Leipp, fondateur de la psychoacoustique en France, autrement dit d'une approche de la musique basée sur la mesure des perceptions des auditeurs. Fabricant de violons, Leipp s'est beaucoup intéressé à cet instrument, mais il a aussi travaillé sur l'acoustique des salles et occasionnellement à l'analyse de musiques extra-européennes. Il a été un soutien enthousiaste de nos travaux. C'est à son Intégrateur de densité spectrale (IDS) que je dois le principe du tonagramme évoqué plus haut.
Quant à Pierre-Yves, il était organiste (élève de Marie-Claire Alain) et accordeur d'instruments (orgues et pianos). Sa thèse « Musique et tempérament », dont il a publié en 2000 une version révisée, portait sur les techniques d'accordage des instruments à sons fixes en Europe à partir du 16e siècle.
La description d'une technique d'accordage est celle d'un processus, autrement dit la construction d'une série d'intervalles qui sonnent particulièrement à l'oreille, par exemple les quintes justes (faciles à vérifier sur ces instruments), mais aussi des quintes légèrement plus grandes ou légèrement plus petites que l'on ajuste en les égalisant entre deux points déterminés.

Agrandissement : Illustration 10

On ne dispose bien sûr pas de fréquencemètre ni de description numérique du résultat à atteindre. L'évaluation des quintes se fait par comptage de leurs battements. Mais, ici encore, la procédure peut être modélisée pour simuler ces techniques d'accordage sur un ordinateur (voir https://bolprocessor.org/creation-just-intonation/).
L'ouvrage de Pierre-Yves Asselin est une description pratique des techniques d'accordage destinée aux joueurs de clavecin qui interprètent le répertoire de musique baroque en Europe. C'est une admirable synthèse de son déchiffrage de documents historiques.
Par conséquent, pour les musiciens occidentaux avant l'arrivée des nombres, l'accord des instruments était réalisé à partir d'expériences auditives semblables à celle que l'auteur du Natya Shastra avait décrite pour la réalisation du pramāņa śruti. Le problème, pour les Occidentaux comme pour leurs collègues indiens, est que la popularisation d'une description numérique, avec la métaphysique des « nombres sacrés » qu'elle réinstallait, a figé le système en imposant un modèle unique qui bien souvent ne correspondait plus à l'expérience musicale.
Avec le déploiement d'orchestres mêlant de nombreux instruments polyphoniques, ces subtilités du système tonal sont passées au second plan. L'harmonie a primé sur la mélodie, à l'agacement de Jean-Jacques Rousseau (ennemi de Rameau) qui proclamait que « le chant français n'est qu'un aboiement continuel, insupportable à toute oreille non prévenue ; que l'harmonie en est brute, sans expression, et sentant uniquement son remplissage d'écolier »… La musique occidentale explorait d'autres dimensions, des notions que, par la suite, les musicologues (occidentaux) ont tenues pour modernes, et forcément « plus accomplies » dans leur vision eurocentrée du monde civilisé.
En réalité, chaque changement de paradigme permait de mettre à l'écart certaines voies pour en explorer d'autres, ce qui est louable tant qu'on ne les considère pas comme une invalidation du paradigme précédent. Le problème de l'enseignement classique de la musicologie, en Occident, est qu'on institue comme une évolution irréversible les inventions de théories du contrepoint et de l'harmonie, qui culminent à la fin du 19e siècle — il va sans dire au sommet de la civilisation (occidentale, il va de soi).
Au 20e siècle, le concept de tempérament s'est réduit à celui du tempérament égal qui n'a aucun fondement musical. C'est un pur arrangement technique : sur un harmonium indien, on peut accompagner n'importe quel raga chanté en choisissant la position de base adaptée à l'interprète et en produisant les mêmes intervalles — qui sonnent « faux » mais que l'oreille ne distingue pas. C'est pratique, mais cela n'a rien d'un perfectionnement musical…
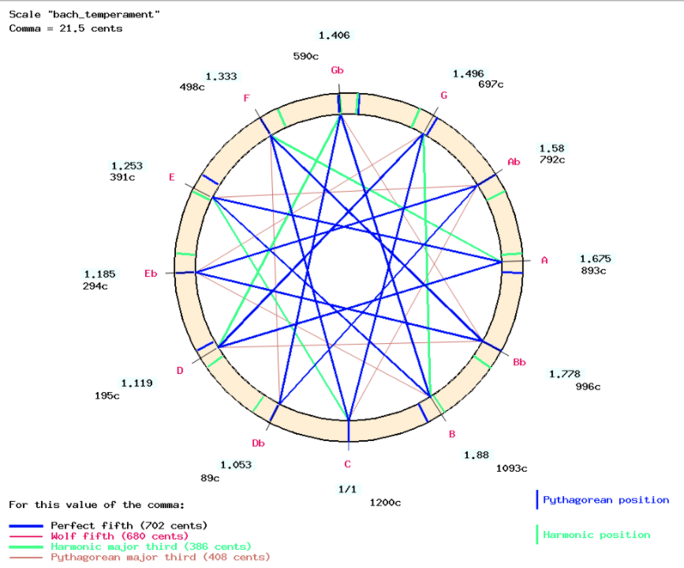
La confusion est telle que de nombreux musiciens sont persuadés que Johannes-Sebastian Bach était un promoteur du tempérament égal, et qu'il a composé à cet effet les préludes de son Clavier bien tempéré.

Mais le tempérament qu'il utilisait en 1722 n'avait rien à voir avec celui du 20e siècle ! Le problème à résoudre est donc : qu'entendait-il par « bien tempéré » ? Je l'ai abordé de manière systématique en important dans le Bol Processor l'intégralité des 96 préludes et fugues du Clavier bien tempéré (livres I et II), puis en recherchant la meilleure parité entre chaque pièce et tous les schémas d'accordage décrits par Pierre-Yves Asselin, plus les gammes naturelles construites sur le modèle de « l'intonation juste » (voir https://bolprocessor.org/just-intonation-framework/ et https://bolprocessor.org/misc/figs/list-scales.php).
Agrandissement : Illustration 12
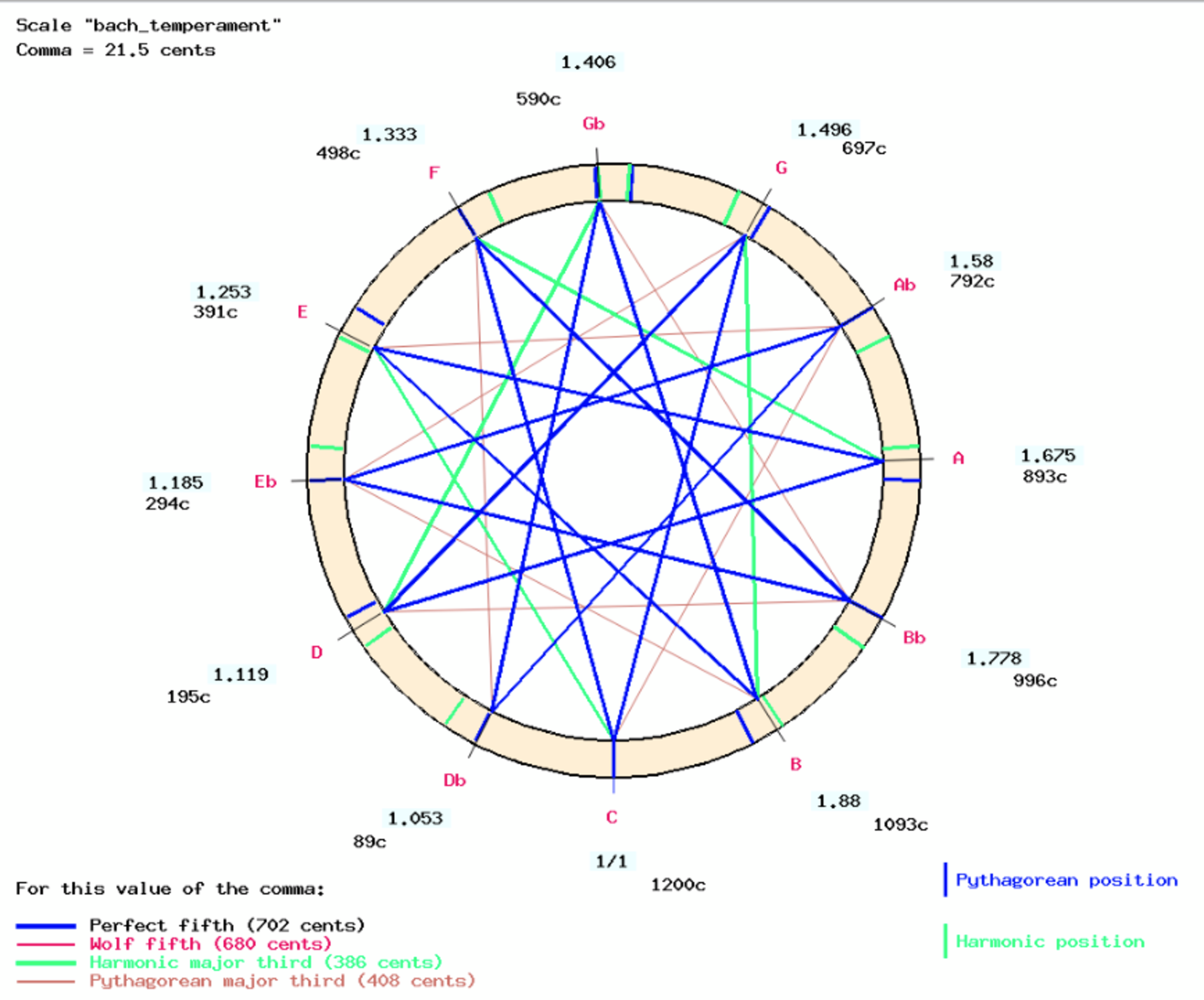
Il fallait pour cela émettre des hypothèses sur les intervalles mélodiques et harmoniques qui répondraient le mieux à la notion de « consonance », à supposer que cette qualité fût celle recherchée par le compositeur. J'ai donc programmé, pour commencer, deux modèles de consonance et publié les résultats de ces aparairages que l'on peut apprécier auditivement en comparaison avec les mêmes œuvres interprétées par des humains sur de véritables clavecins : https://bolprocessor.org/the-well-tempered-clavier/
Une autre approche comparative est celle de l'article “Comparing temperaments” (https://bolprocessor.org/comparing-temperaments/). Quand on interprète « Les Ombres Errantes » de François Couperin, il est raisonnable de faire appel à un tempérament conçu à la même époque par Jean-Philippe Rameau. Effectivement, on peut entendre que le tempérament Rameau en sib donne une qualité stupéfiante à cette œuvre musicale (version synthétisée : https://bolprocessor.org/misc/sounds/Ombres_errantes_rameau_en_sib.mp3). Ici, l'information historique (proximité entre Couperin et Rameau) est appuyée par la proximité tonale (calculée) de l'œuvre et de ce tempérament.
Avec une telle subtilité de l'intonation, on se situait, en Occident, dans le même registre que les maîtres indiens de rudra vina. Il n'y a donc pas de différence fondamentale entre l'approche de l'intonation en Inde et en Europe, pourvu que l'on revienne sur cette notion en se détachant de la mystique des nombres… Mathias Enard, auteur du magnifique roman Boussole (prix Goncourt 2015), déclarait dans un entretien :
Interroger la frontière, c’est comprendre ce qu’elle est, où elle passe, montrer sa mobilité mais ne pas la nier. On ne peut pas nier la différence, et d’ailleurs la différence est aimable. Quant à l’idée du “monde entre les mondes”, elle nous vient de la mystique musulmane. C’est l’image du “barzakh”, l’intervalle, ce monde qui ne serait ni ici ni ailleurs, ni soi ni l’autre, mais entre les deux. Qui serait capable d’intégrer l’autre en soi et le soi dans l’autre. On pourrait rêver d’un orientalisme idéal ; il serait ce monde entre les mondes.
Publications
- Arnold, E. J. A Mathematical model of the Shruti-Swara-Grama-Murcchana-Jati System. New Delhi, 1982: Journal of the Sangit Natak Akademi.
- Arnold, E.J.; Bel, B. A Scientific Study of North Indian Music. Bombay, 1983: NCPA Quarterly Journal, vol. XII Nos. 2 & 3.
- Arnold, E.J.; Bel, B. L’intonation juste dans la théorie ancienne de l’Inde, ses applications aux musiques modale et harmonique. Revue de musicologie, JSTOR, 1985, 71e (1-2), p.11-38.
- Asselin, P.-Y. Musique et tempérament. Paris, [1985] 2000 : Jobert.
- Bel, B. A Mathematical Discussion of the Ancient Theory of Scales according to Natyashastra. Note interne, Groupe Représentation et Traitement des Connaissances (CNRS), March 1988a.
- Bel, B. Raga : approches conceptuelles et expérimentales. Actes du colloque « Structures Musicales et Assistance Informatique », Marseille 1988b.
- Rao, S.; Van der Meer, W. The Construction, Reconstruction, and Deconstruction of Shruti. Hindustani music: thirteenth to twentieth centuries (J. Bor). New Delhi, 2010: Manohar.
- Raju, C. K. Cultural foundations of mathematics : the nature of mathematical proof and the transmission of the calculus from India to Europe in the 16th c. CE. Delhi, 2007: Pearson Longman: Project of History of Indian Science, Philosophy and Culture : Centre for Studies in Civilizations.
Remerciements
Ces travaux ont bénéficié de divers financements du Fonds International pour la Promotion de la Culture (FIPC/UNESCO), de Sangeet Research Academy (Kolkata), du National Centre for the Performing Arts (Mumbai), de la Ford Foundation (USA), et bien sûr, au final, de mon emploi au CNRS… mais — malgré plusieurs tentatives — aucun soutien du Ministère de la culture en France, si ce n’est une bourse Romain Rolland qui m’a permis de renouveler mon visa et le stock de cassettes audio !
Le premier financement (UNESCO) a été accordé grâce au soutien de gens passionnés, attentifs à nos propositions ambitieuses et curieux de les voir aboutir : Émile Leipp, Jean During, Iannis Xenakis, Alain Daniélou, Gilbert Rouget, et j’en oublie…



