Les photos d'insectes sont tirées du livre Microcosmos, et donc du film.
Paradoxes connus, le vide, le zéro, le néant, et leurs corollaires, l’univers, la valeur, l’être.
Mystères ancestraux. Si Dieu explique l’existence de ce qu’il a créé, qu’est-ce qui explique Dieu ?
Est-ce la poule qui philosophe, ou bien l’œuf qui philopole ? Le mystère des causes premières. Sapiens de chez sapiens est fier d’avoir dit le Big Bang. Mais qu’est-ce qui a produit le Big Bang ? Épicure, très tôt expose le principe qui sera celui de Lavoisier : rien ne sort de rien. Rien ne disparaît. Tout se transforme. Ses écrits, probablement victimes d’autodafés, tant ils étaient blasphématoires, ont disparu. Sa philosophie est calomniée dès le départ. « Pourceaux d’Épicure ». « épicurien » signifie aujourd’hui quasiment le contraire de son sens véritable. L’essentiel de sa pensée ne nous est parvenue que grâce à Lucrèce, De natura rerum. La nature des choses. Res, rei : chose, être, affaire, fait, événement, circonstance… Notre « rien » français en vient (de l’accusatif, « rei »).
Ces gens ne sont rien ? Quelle sottise. Les gens sont riens. Les gens sont gens. Les gens sont personnes.
Je ne suis rien ? Quoiqu'en pense le maire de Conflans qui raye ma librairie-école sans même m'en aviser, je suis rien : je suis quelqu'un.
En poème liminaire à un aride torride exposé mathématique, voilà un petit poème de rien du tout :
Naissances
Le ciel retient son souffle à chaque vie qui prend.
Pour lui, toute naissance est un évènement:
Une étoile, un enfant, un faon, un éléphant,
Baleine, écureuil, fleur, girafe ou froment.
Tout retentit, sans fin, dans l'univers immense,
Et l'agneau étonné qui sur la paille danse,
S'essayant à marcher pour la première fois,
Compte autant que l'aîné dans le berceau des bois.
Les anges, ce matin, comme des chats ronronnent,
Se racontant, joyeux, la belle information :
Sur la Terre, là-bas, pareille à une pomme,
Près d'un ruisseau sans nom est né un hanneton.
Marc Alyn, L'arche enchantée

Agrandissement : Illustration 1

Comment se peut-il que quoi que ce soit existe ? Puisque toute chose ne peut naître que de quelque autre chose.
Une esquisse de réponse est donnée à mon avis par les maths ! Les maths qui formulent des idées telles que l’infini, par exemple. Et un infini qui s’enroule sur lui-même, se contorsionne, et existe en allant aussi bien vers le grand à l’aide d’un télescope, que vers le petit avec un microscope. Instruments d’ailleurs vite dépassés, mais relayés par l’imagination humaine. Et ce qui semble bien résoudre le paradoxe de l’être, qui ne devrait pas être, mais qui est quand-même, c’est l’idée d’infini. En effet, se demander ce qu’il y avait avant, c’est explorer l’infini du passé. Et comme Niteucheu l’a poétisé, c’est aussi induire le devenir.
Un truc qui m’avait frappé en première, c’est la notion d’asymptote. Deux courbes qui se rapprochent indéfiniment, qui ne cessent de se rapprocher, sans jamais s’atteindre.
La fonction inverse
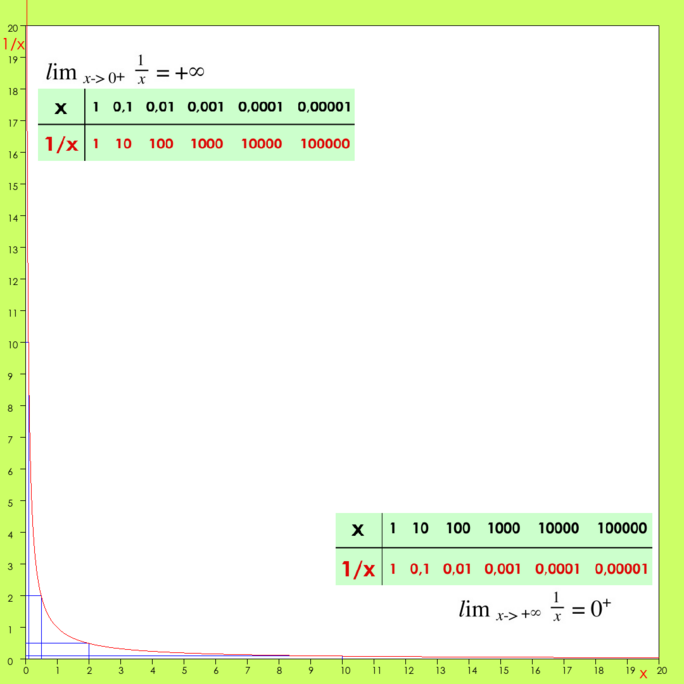
Voici la courbe représentative de la fonction qui à x associe son inverse 1/x. L'axe horizontal représente x, et le vertical 1/x. Les nombres 2 et 10 sont pris en exemple pour montrer le principe de la représentation (voir les lignes bleues). On constate que la courbe, non-seulement s'écarte peu des axes, mais s'en approche à l'infini.
Agrandissement : Illustration 2
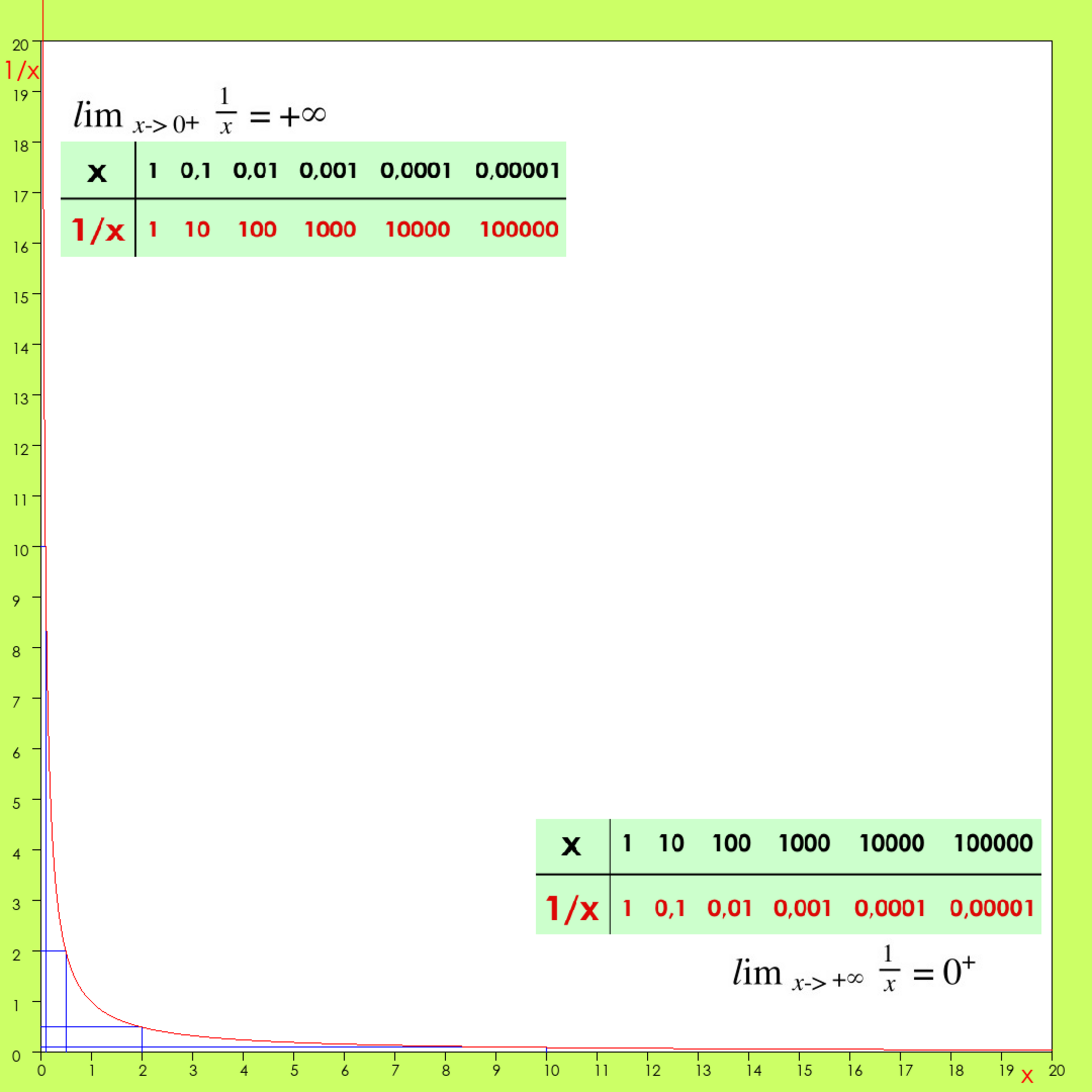
Notion de limite. La limite de l’inverse de x (1/x), quand x tend vers l’infini, est zéro. Et la limite de 1/x quand x tend vers 0, est l’infini. La courbe de la fonction inverse est donc asymptote aussi bien à l’axe horizontal qu’à l’axe vertical. Pour elle, le zéro et l’infini sont reflets l’un de l’autre.
Deux occurrences de la même notion ? Deux avatars du mystère. Et aussi du mystère humain. La littérature butine depuis lurette cette antithèse. Michelet par exemple, lassé de l’histoire humaine, prenant sa retraite en histoire naturelle, sous-titre ainsi L’insecte : l’infini vivant. Le docteur Céline, misan-philanthrope, prononce : L’amour c’est l’infini mis à la portée des caniches. La politique s’en empare, sporadiquement. Des peuples sont le sel de la terre tandis que d’autres doivent être anéantis. « Pays de merde » de Trump. « Gens qui ne sont rien. » L’être, coincé entre ces deux océans, le petit et le grand, penche vers l’un, vers l’autre, et revient à l’équilibre. Et recommence.
La théorie des cordes, c’est-à-dire l’état actuel de la recherche fondamentale en physique, fait l’hypothèse de « dimensions cachées » : confinés et enroulés dans des recoins de particules infimes, se trouveraient des univers. À l’inverse, ce gros Big Bang dont on se demande s’il va finir par s’inverser et se replier sur lui-même évoque une particule ondulatoire, parmi d’autres.

Agrandissement : Illustration 3

Une autre surprise nous attend en terminale, avec la notion d’intégrale. Pour faire simple, une intégrale, c’est une somme d’aires ! Calculer la surface sous une courbe, c’est tranquille si la courbe est droite ! Parce qu’on sait calculer l’aire de n’importe quel polygone. Mais si c’est courbe ? Eh ben c’est faisable quand-même ! Grâce à la notion de limite. On va ajouter de plus en plus de rectangles, de plus en plus petits, jusqu’à l’infini ! Jusqu'au double infini : nombre infini de rectangles, et largeur infiniment petite, c'est-à-dire nulle, de chacun des rectangles. Et cette aire qui existe, bien qu’on ne puisse la calculer avec les maths de collège, on va la trouver ! Ce sera la somme d’un infini de fois zéro ! Oui. En ajoutant zéro sans cesse, on construit une aire. On crée. Et de cette arrivée sur les confins de l’infini va naître en même temps la réalité de cette aire, et la valeur que l’on cherchait. Il se confirme que c’est la notion d’infini qui permet de casser le paradoxe de l’être et du non-être !
Approximation de Pi interprété comme une aire
Agrandissement : Illustration 4
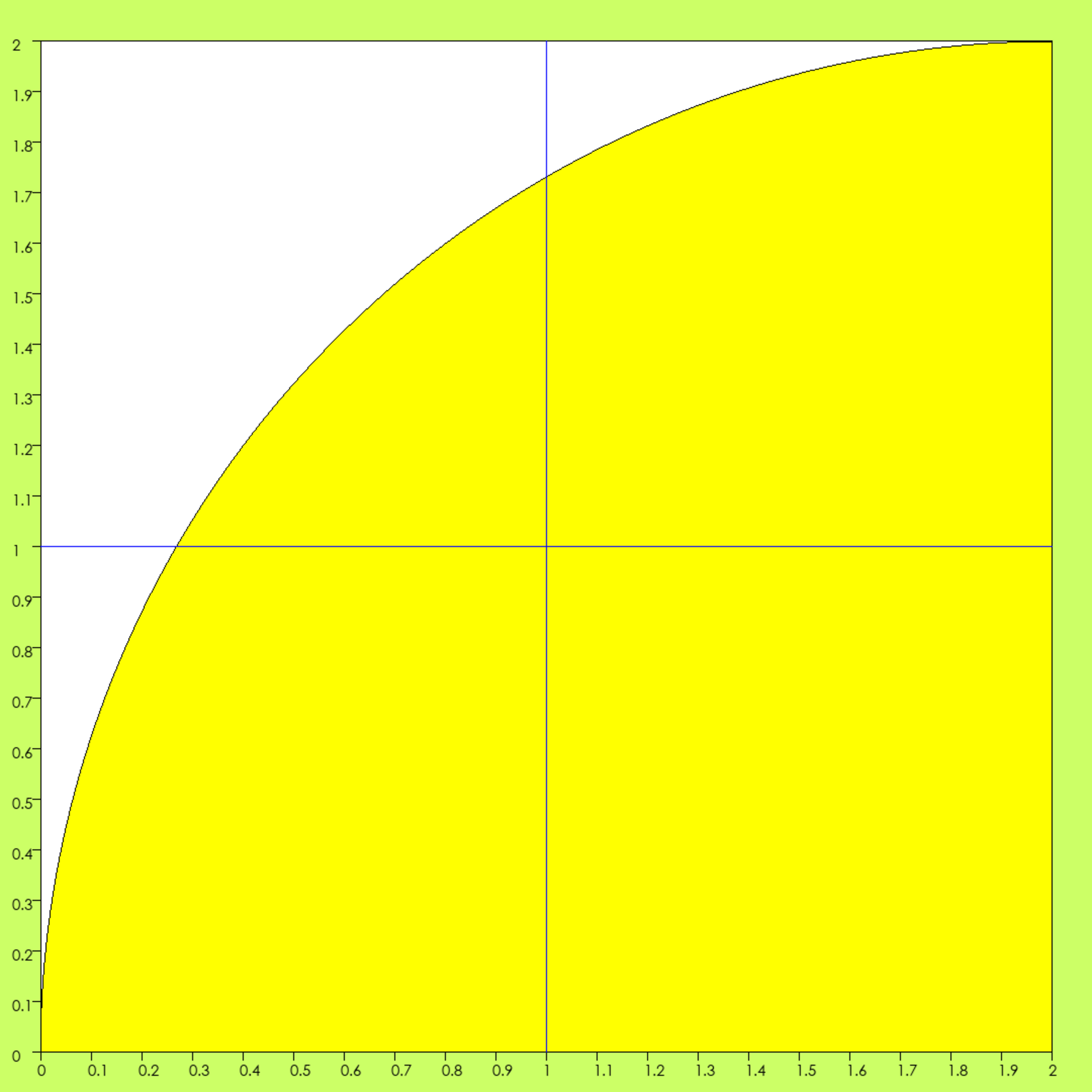
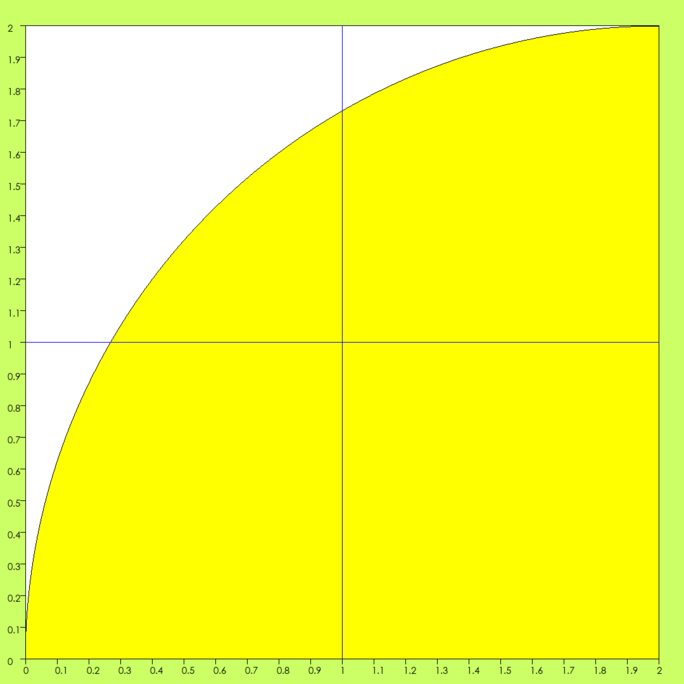
Cette aire jaune a une surface égale à Pi, si on compte en « unités d’aire » correspondant au carré de côté 1, par exemple celui qui est en bas à droite, qui a une aire égale à 1, raison pour laquelle on va le prendre comme « unité d’aire », u.a). Les unités d’aire, c’est simple : elles dérivent des unités de longueur. Un carré de côté 1cm, a pour aire 1 cm 2. Un carré de côté 1 m, c’est 1 m 2. Une unité d’aire est l’aire d’un carré dont le côté est égal à une unité de longueur.
L’aire jaune est un quart de cercle, inscrit dans un carré de côté 2 qui a donc une aire égale à 4 u.a. Vous pouvez évaluer à peu près l’aire jaune. On a un carré un peu entamé en bas à gauche, un autre entamé de la même façon en haut à droite. Mais ce qui reste du carré en haut à gauche fait un peu plus que compenser ce qui manque dans les deux derniers. L’aire du quart de disque jaune est donc supérieure à 3. En fait, elle est égale à 3,14 3,142 3,1416 3,14159 merdre ! Elle n’est égale à aucun nombre décimal. La suite des décimales de Pi est infinie, non périodique, complètement aléatoire. Un petit poème vous donne les premières, son premier vers en fournit onze :
Que j’aime à faire connaître ce nombre utile aux sages ! …
Comptez le nombre de lettres de chaque mot : 3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5… Ma calculette Casio est déjà prise en défaut à ce stade : elle donne dix chiffres seulement ! Et comme elle suit la règle d’arrondi, elle donne comme dixième chiffre 4 au lieu de 3, puisque le suivant est 5.
Je ne sais plus combien de chiffres donne le poème entier. Plusieurs centaines, je crois. Aujourd’hui, grâce aux ordinateurs, on en connaît des milliards. Il suffit de trouver une suite qui tend vers Pi. Tendre vers Pi, pour une suite, infinie bien sûr, cela signifie que chaque nouvelle valeur s’approche un peu plus, sans toutefois qu’on n’y arrive jamais, puisque justement, c’est infini ! Une suite qui tend pépère vers Pi, c’est le périmètre d’une suite de polygones inscrits dans un cercle de diamètre égal à 1, dont le nombre de côtés croît. Forcément, le périmètre s’approche de celui du cercle, égal au produit de Pi par le diamètre, donc Pi. Pour un carré inscrit, on est à 2racine(2), dans les 2,8 ; pour un hexagone, on est déjà à 3 ! On peut aller un peu plus vite vers Pi en doublant le nombre de côtés à chaque fois. Mais c’est pas très rapide non plus. On trouve sans cesse de nouvelles suites qui permettent de foncer plus vite, sans jamais l’atteindre, bien sûr, et on en est aujourd’hui à plus de 30000 milliards de sabords décimales de Pi !
Ce que je vais vous montrer maintenant, c’est une suite d’aires qui va tendre vers l’aire du quart de disque jaune. L’aire du cercle entier, de rayon 2, serait égale à Pi x 2 au carré, si vous vous souvenez de ce cours de CM2. Donc Pi fois 4. Donc le quart de disque a une aire égale à Pi. Chacune des images qui viennent vous montre donc une approximation de plus en plus fine, par valeur inférieure, de Pi.
Agrandissement : Illustration 5
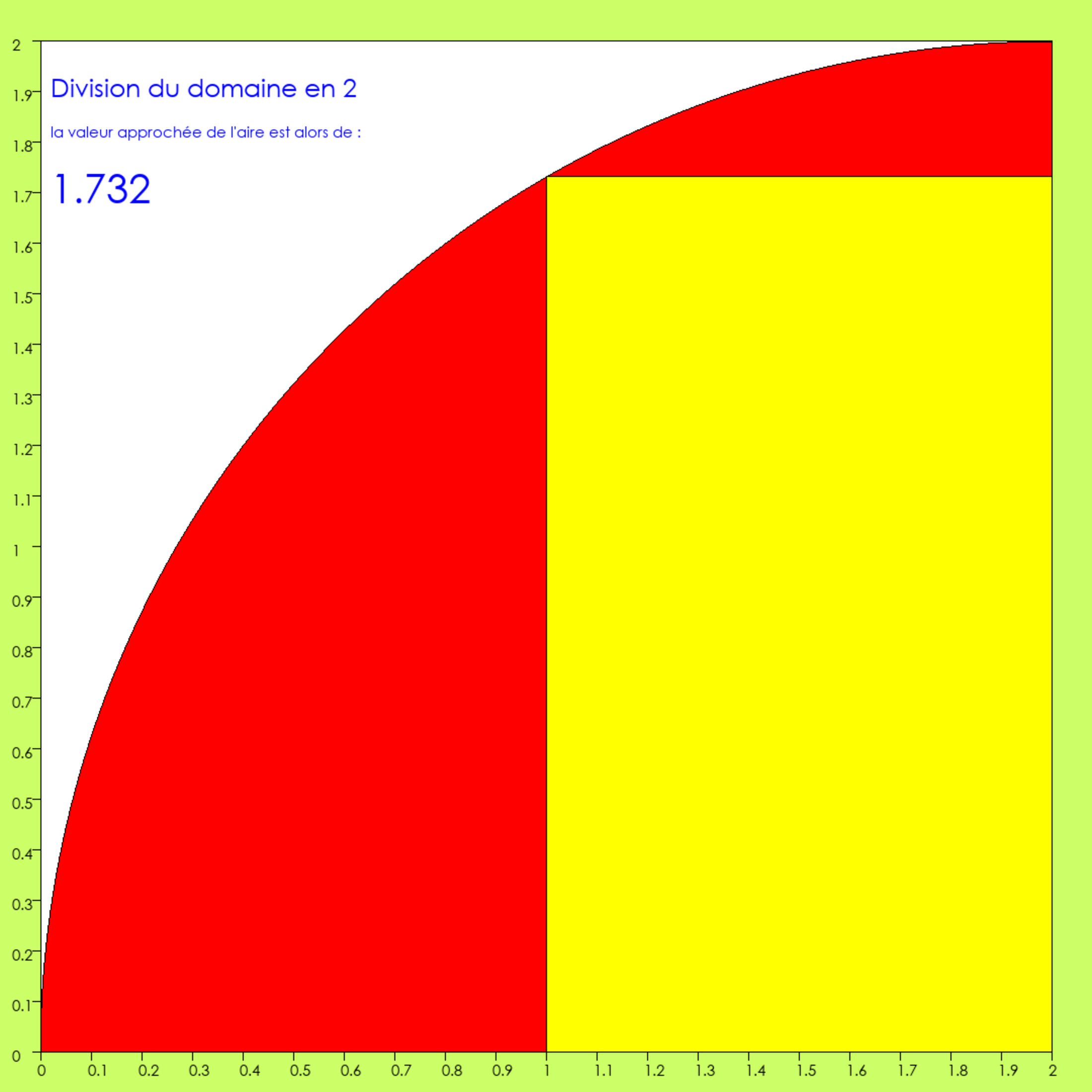
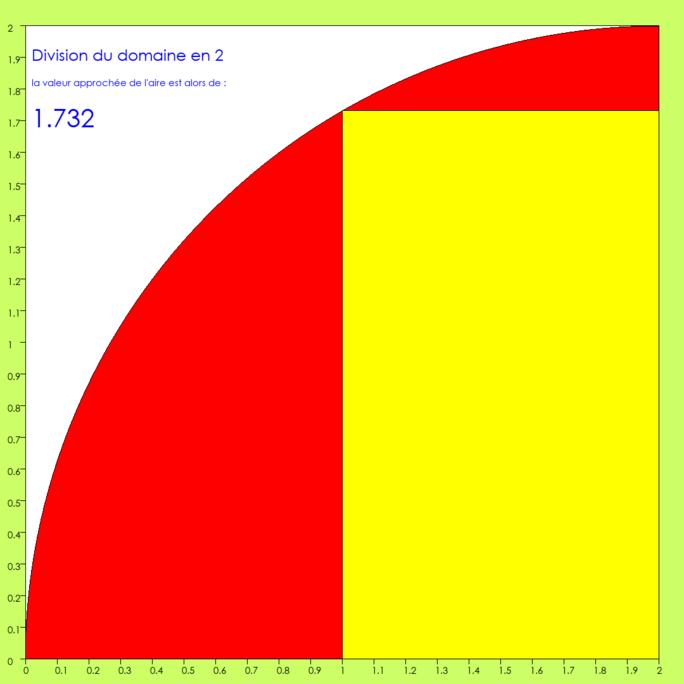
Le « domaine », l’intervalle [0 ; 2], horizontal, qui sert de base au quart de disque est divisé en 2 parties. Sur chacune de ses parties, on construit le plus haut rectangle possible : il a pour base la moitié du domaine, pour hauteur la hauteur à laquelle il touche le cercle. En fait, là, on n’a qu’un rectangle. En effet, le cercle commençant à la hauteur zéro, la hauteur du premier rectangle est zéro.
L’approximation est fort grossière, l’erreur énorme : elle est représentée en rouge. Sur les quelques 3,14… u.a. du quart de disque, ne sont comptées que 1,732 u.a. Cette valeur résulte de ce calcul : 1.0x0.0 + 1.0x1.732
Agrandissement : Illustration 6
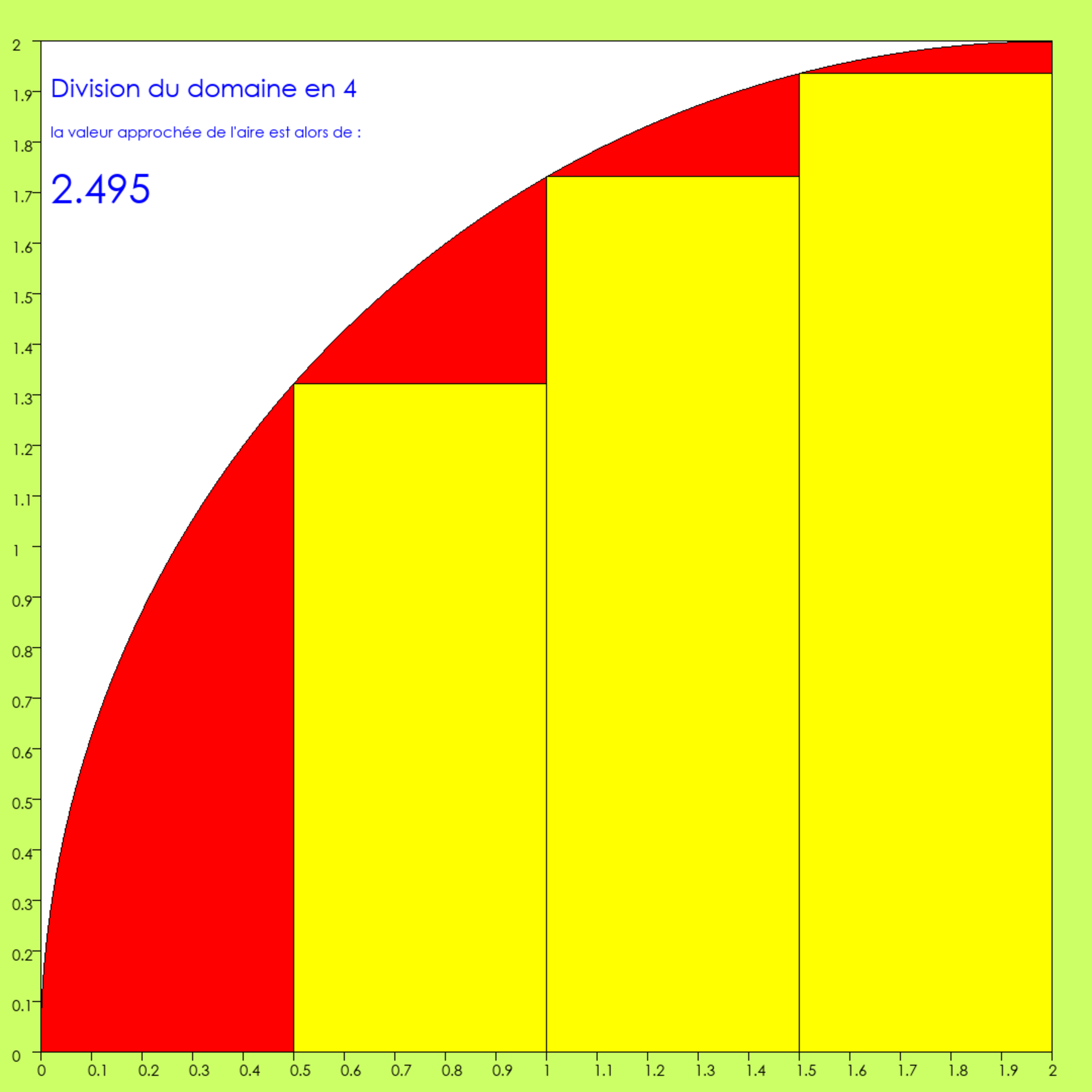
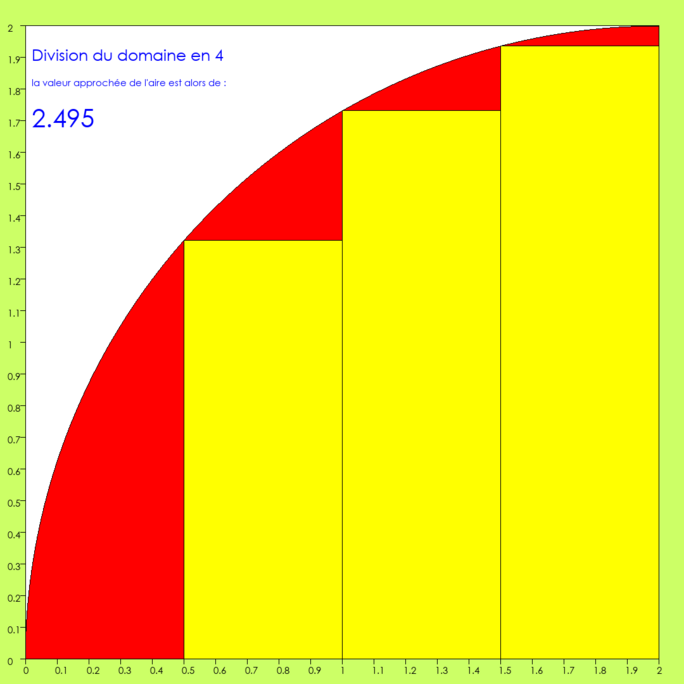
C’est mieux ! Le domaine est divisé en 4 parties. On a toujours un rectangle de moins que de subdivisions. La zone rouge diminue, la zone jaune augmente. Moins d’erreur, meilleure approximation. La nouvelle valeur résulte de ce calcul : 0.5x0.0 + 0.5x1.322 + 0.5x1.732 + 0.5x1.936
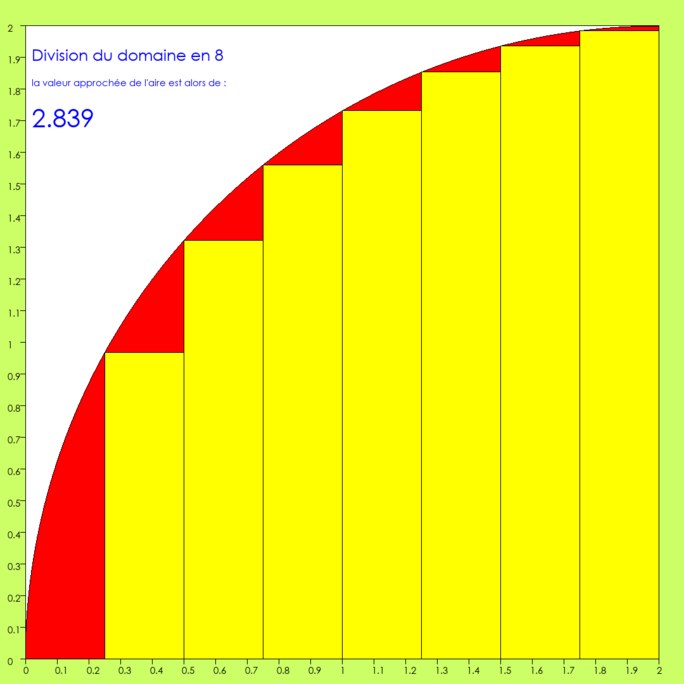
Agrandissement : Illustration 7
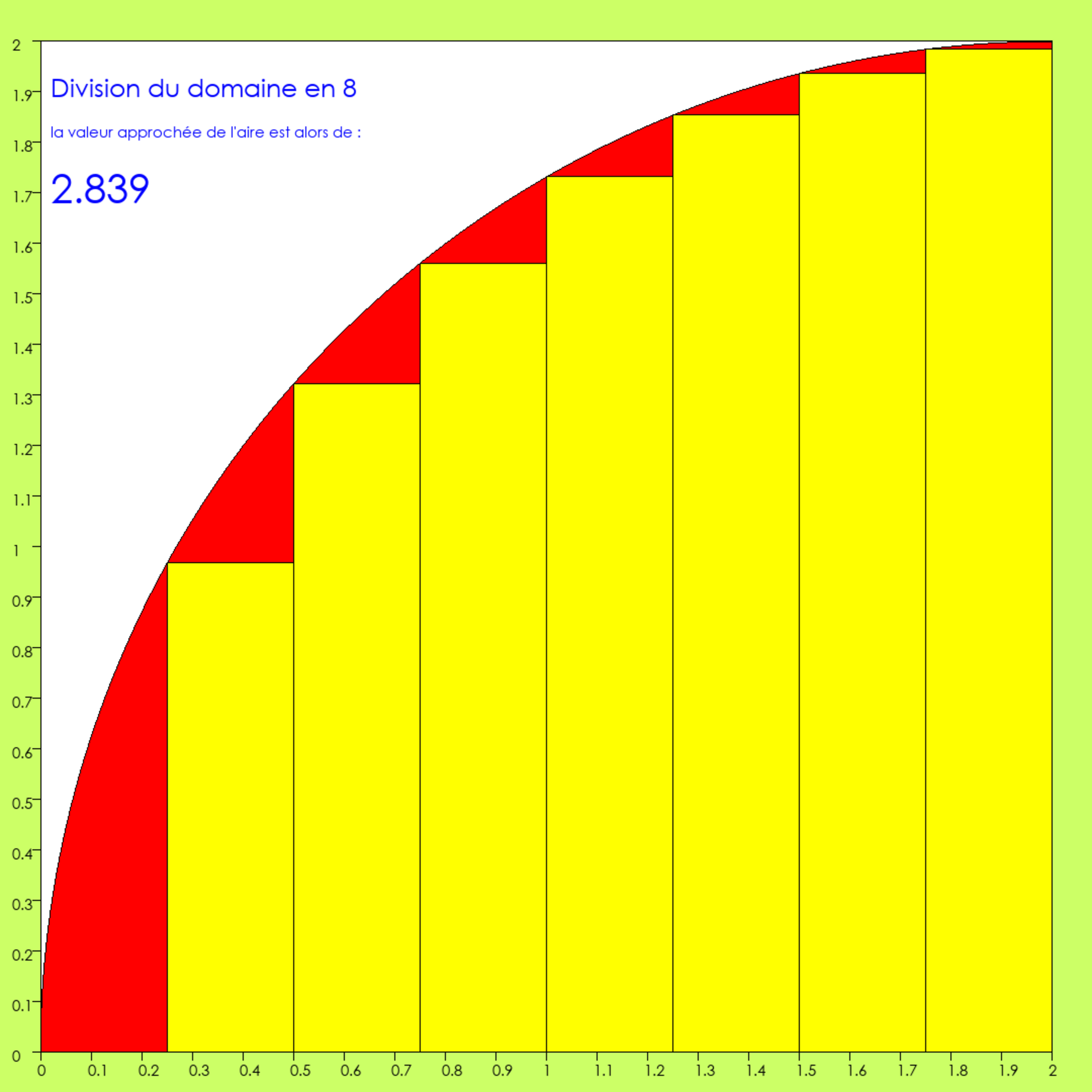
La rouge erreur continue de s’amenuiser.
0.25x0.0 + 0.25x0.968 + 0.25x1.322 + 0.25x1.56 + 0.25x1.732 + 0.25x1.854 + 0.25x1.936 + 0.25x1.984
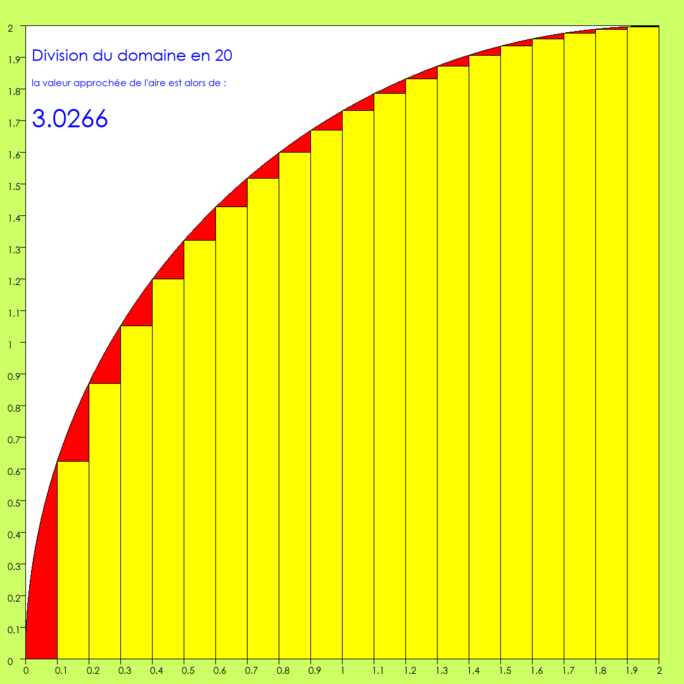
Agrandissement : Illustration 8
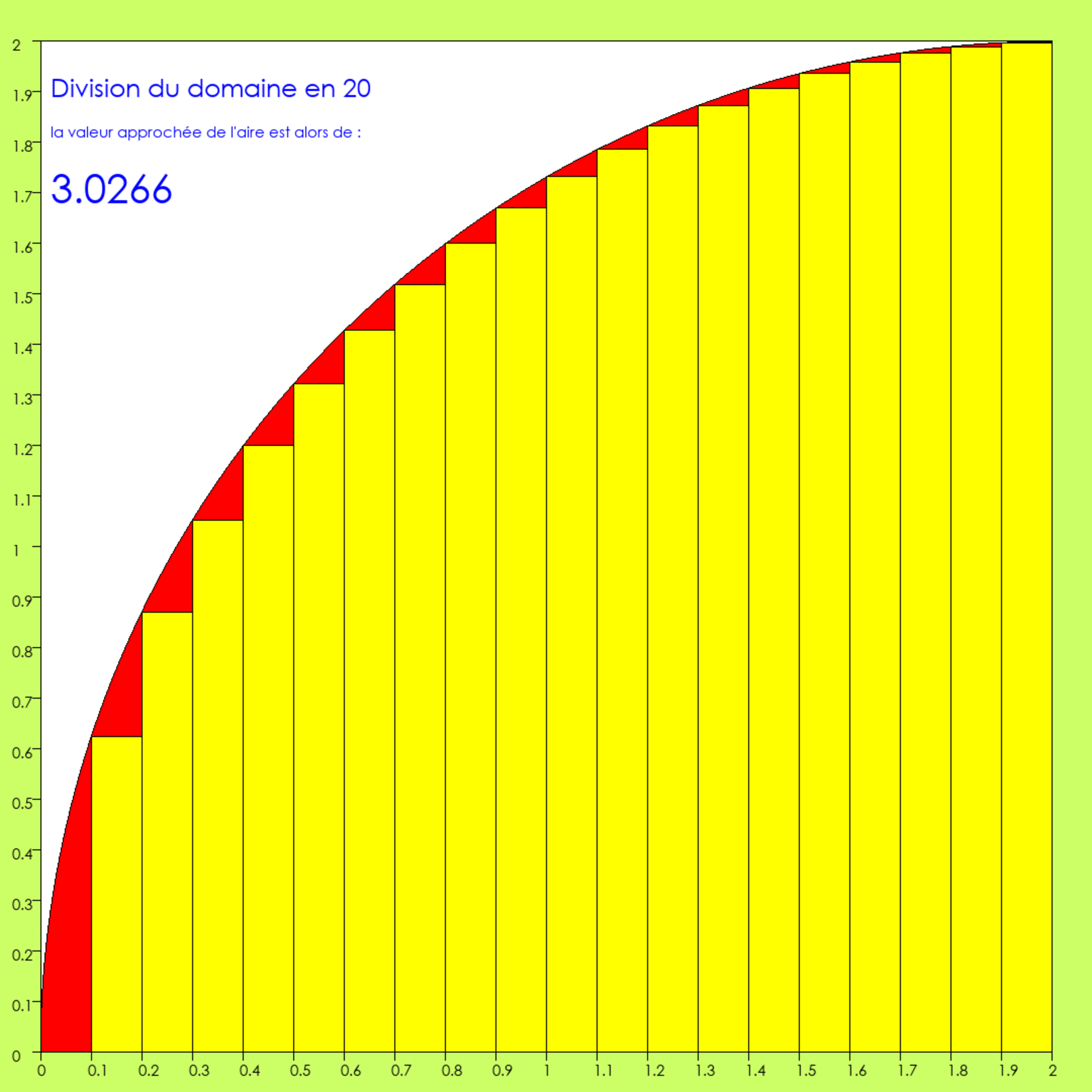
On commence à sentir l’écurie. L’approximation de Pi dépasse 3 !
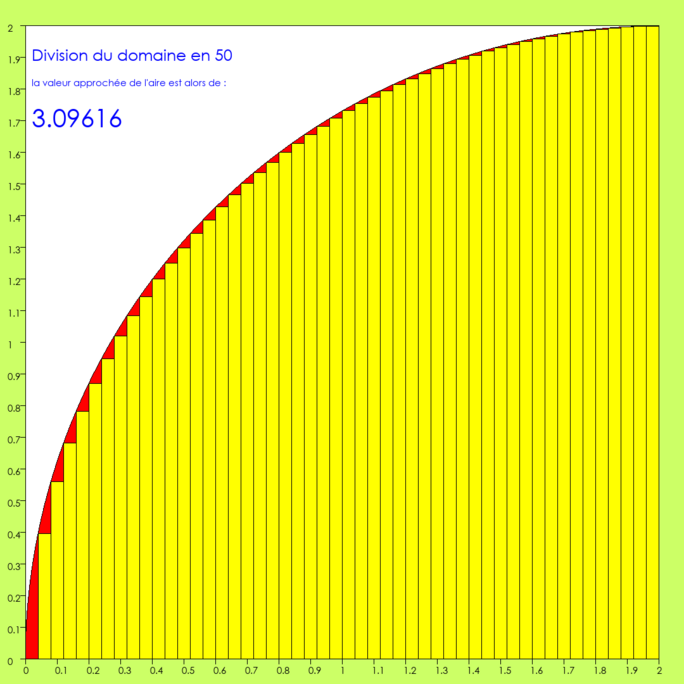
Agrandissement : Illustration 9
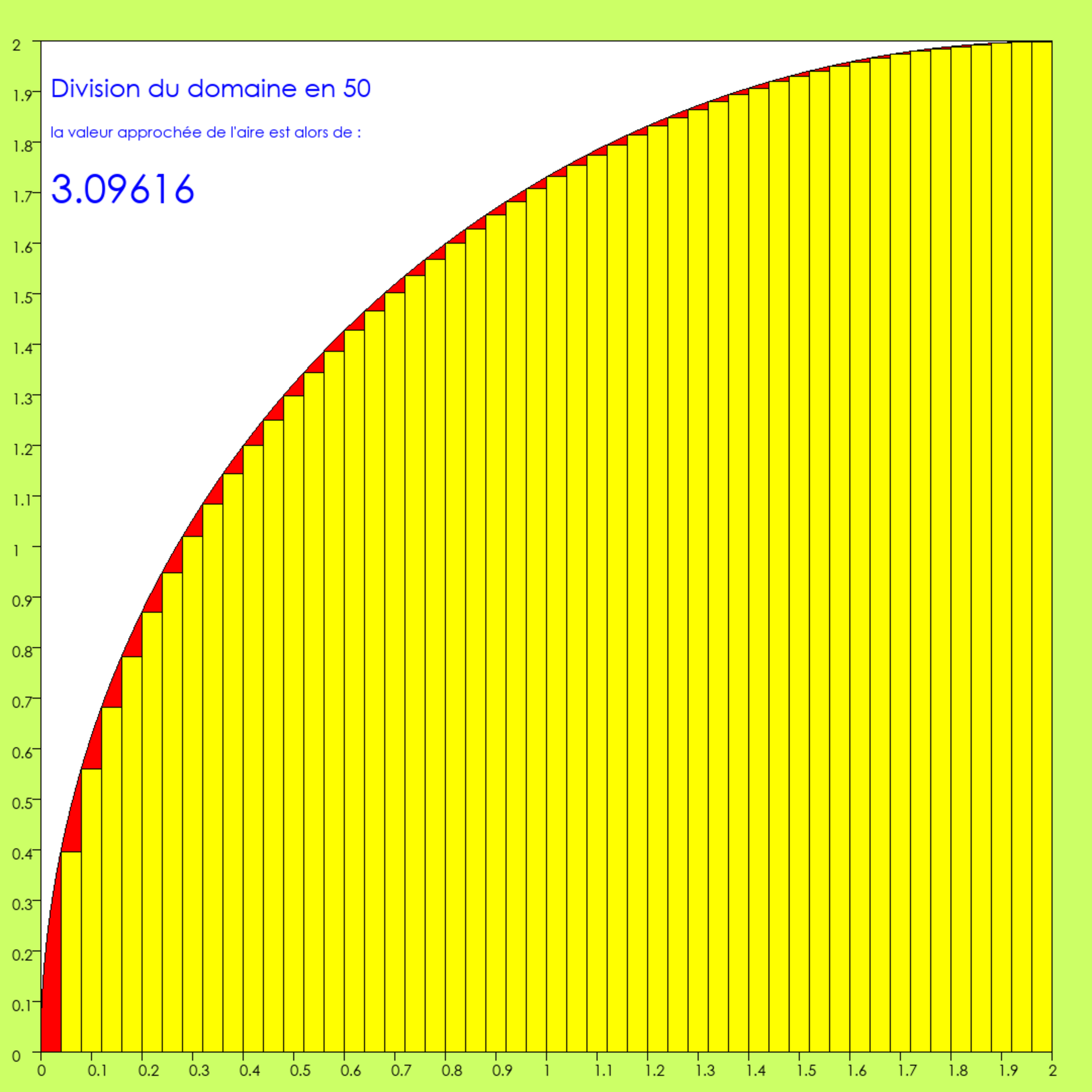
Dans les trois rectangles de droite, l’erreur est devenue inférieure au pixel, et on ne la voit donc plus (elle existe cependant, mathématiquement).
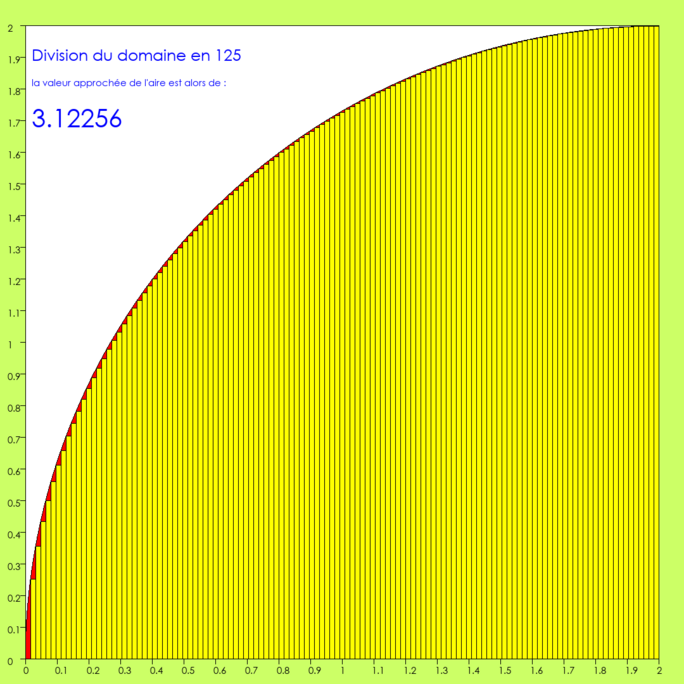
Agrandissement : Illustration 10
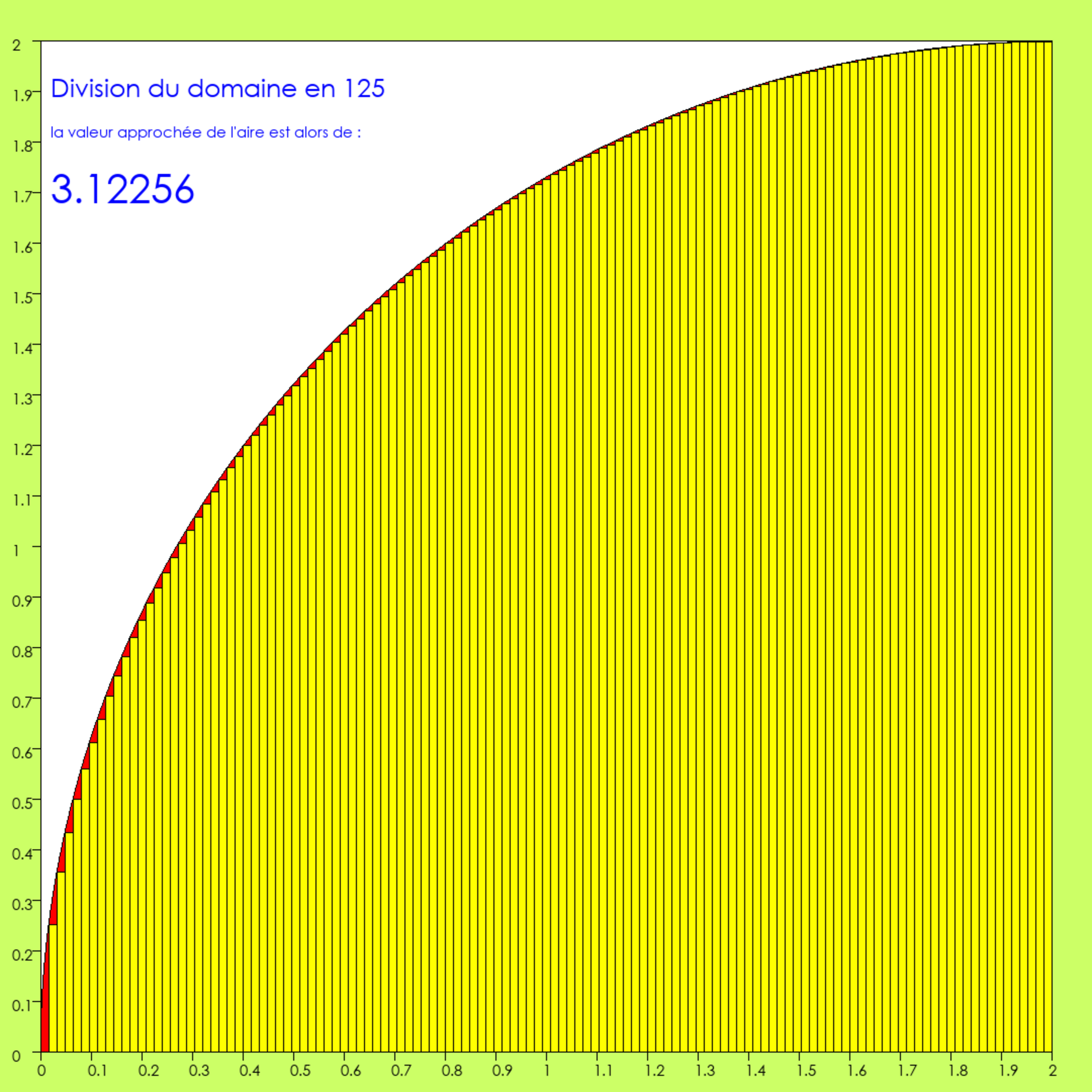
La première décimale est atteinte !
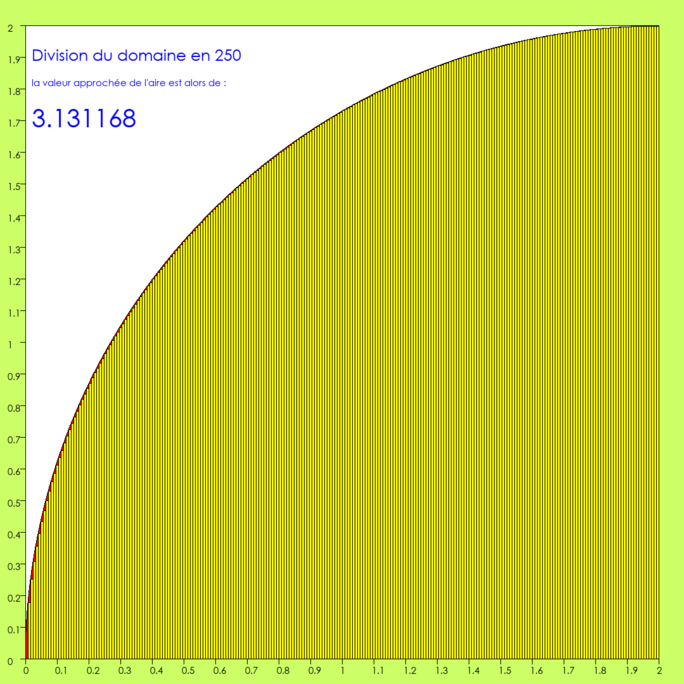
Agrandissement : Illustration 11
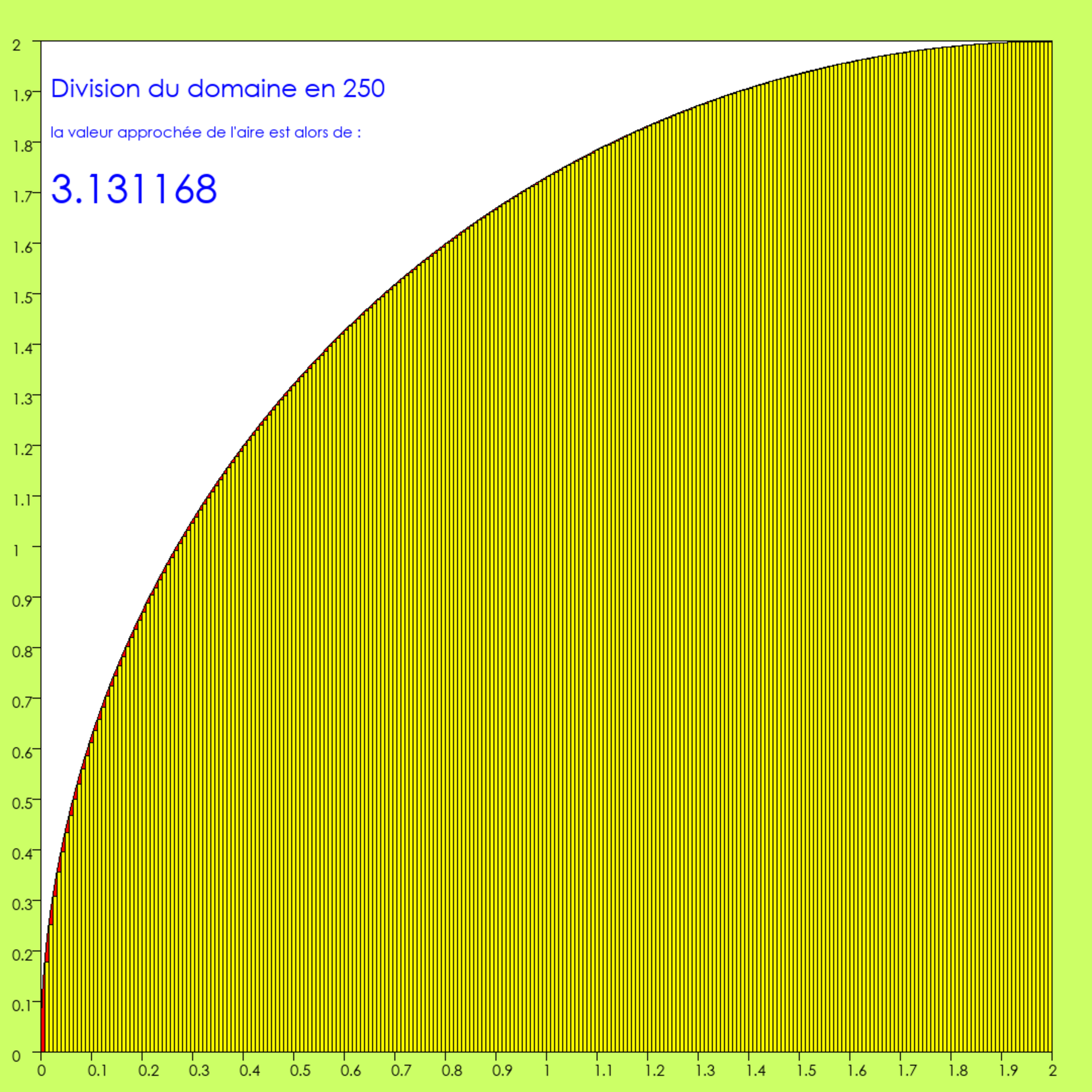
C’est environ une soixantaine de rectangles qui ne sont plus surmontés de rouge ! Comme depuis le début, il n’y a pas de rectangle N° 1, et c’est toujours à cet endroit qu’on a la plus grande erreur. Mais elle aussi ne cesse de décroître depuis le début.
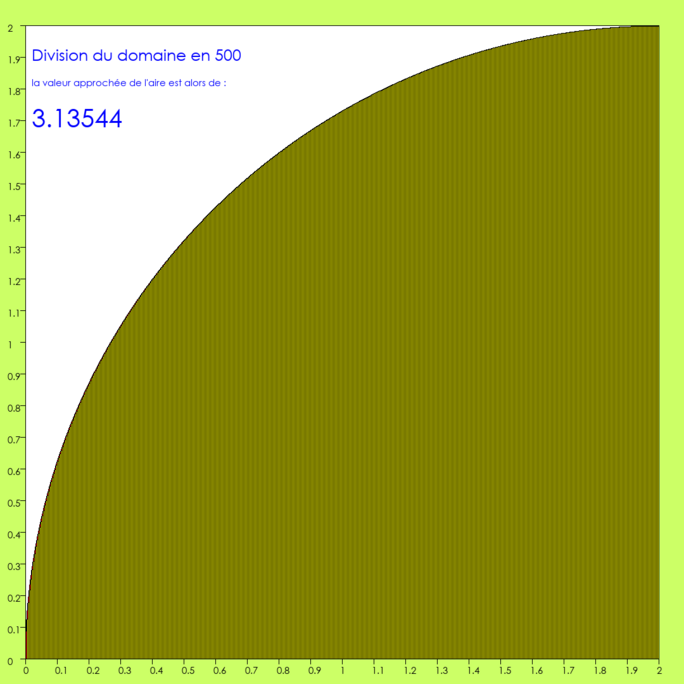
Agrandissement : Illustration 12
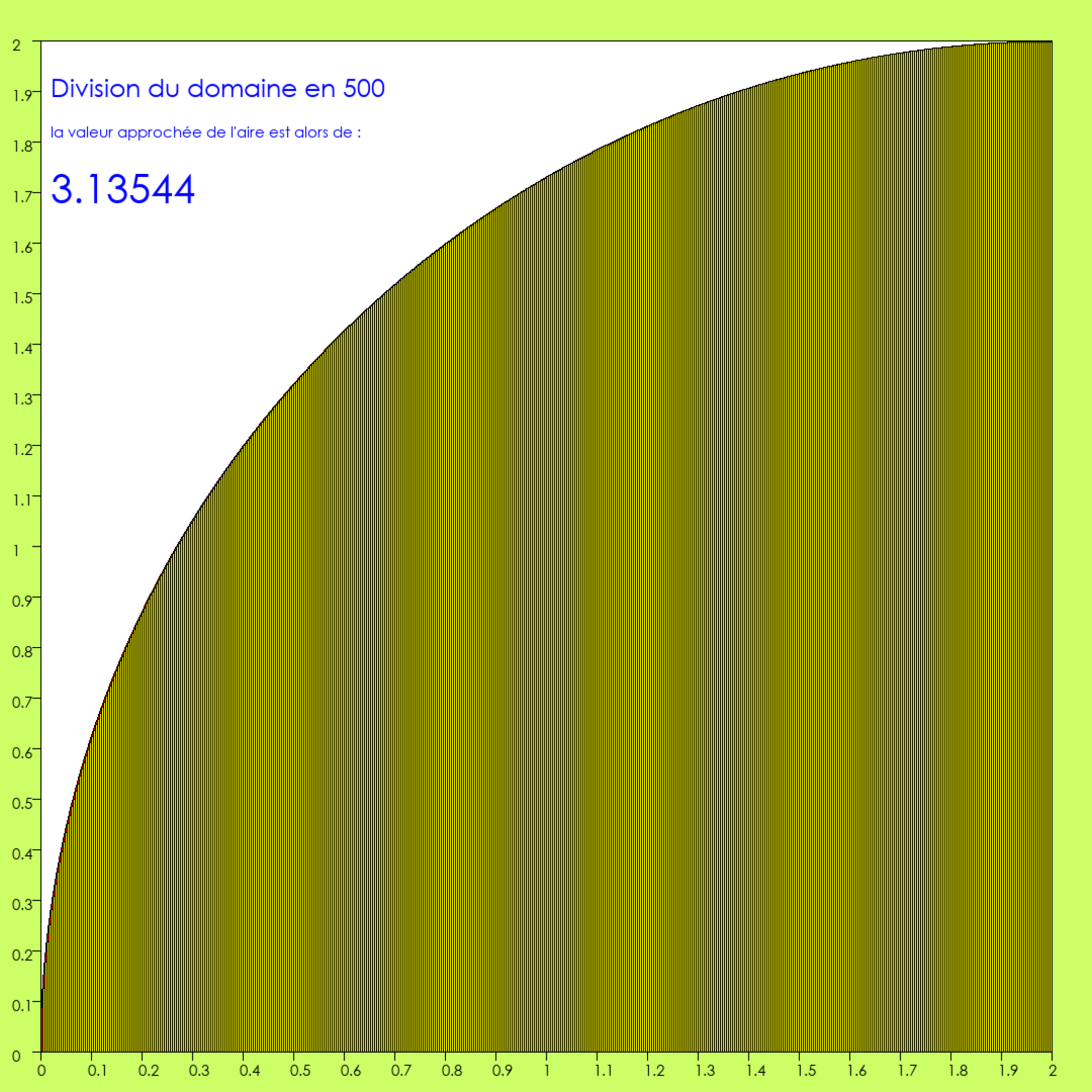
Pour une moitié des rectangles, l’erreur est inférieure au pixel, et est donc invisible.
On n’est pas arrivé à la deuxième décimale de Pi, tout au plus peut-on dire que si on arrondit notre approximation à la deuxième décimale, ça donnera 3,14, puisque la troisième décimale est 5.
La zone jaune est considérablement assombrie, c’est à cause des lignes noires qui séparent les rectangles. En effet, la base étant de 1000 pixels, divisée en 500, la base d’un rectangle est 2 ! Il en faut un pour tracer la ligne noire. Il n’en reste qu’un en jaune !
L'idée que la valeur exacte de l'aire sous la courbe d'une fonction f entre deux valeurs a et b de la variable x se calcule de cette façon est ainsi formulée :
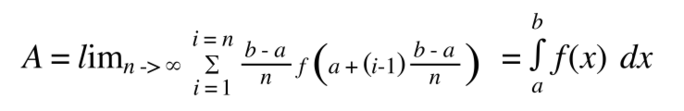
Agrandissement : Illustration 13
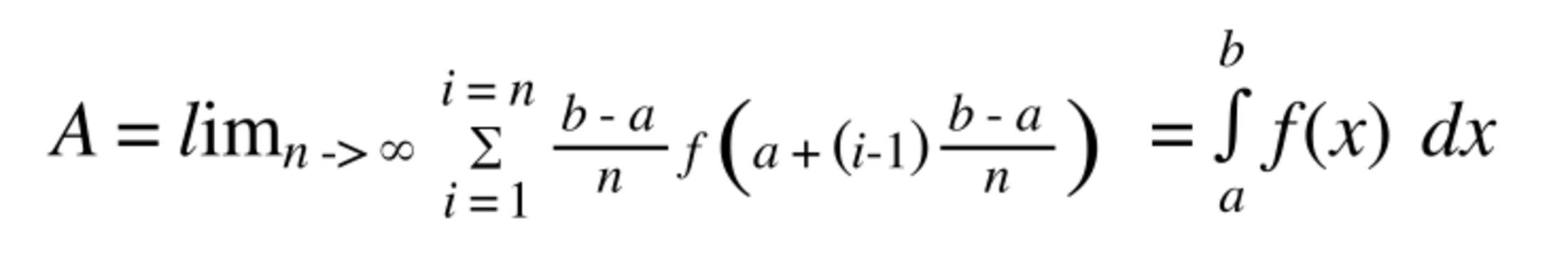
Le signe sigma majuscule signifie "somme". La partie située à droite, jusqu'au signe "égal", exprime l'aire d'un rectangle, de largeur "delta x", le domaine (b - a) divisé par le nombre de rectangles, de hauteur la valeur prise par la fonction pour la valeur extrême-gauche de x. On commence avec i = 1, c'est-à-dire un seul rectangle. Puis on augmente la valeur de i. On obtient une suite de valeurs, une suite d'aires, comme dans l'exemple du quart de cercle. Cette suite est infinie, puisqu'il est toujours possible de subdiviser encore plus. Et la limite de cette suite, souvent calculable par des procédés mathématiques, donne la valeur exacte de l'aire. Elle est exprimée à droite du deuxième signe "égal" = Le sigma est devenu cette sorte de "s", qu'on appelle aussi le "signe somme". Il est affublé des bornes de l'intervalle sur lequel on intègre, et le "delta x" est remplacé par le signe "dx" qui signifie différence "infinitésimale", qui signifie zéro.
Grâce à mon désir de partager ces spéculations philosophico-mathématico-entomologistes, je me suis enfin remis à Python ! Mon projet de logiciel d'entraînement ludique aux mathématiques est en effet arrêté depuis le gros coup de blues consécutif à la négation de mon travail par la puissance publique. Je vais donc terminer avec quelques petites choses qui montrent que de nos jours il est facile de se former, de résister, de construire, d'inventer. C'est facile pour les gens. Pas pour les politiques, apparemment. Eux ne savent guère que détruire ce qui se trouve sur la route de leurs carrières. En toute imbécilité, souvent. Alors que nous, les gens, nous sommes le vrai sel de la terre.
Ce sont les hommes, pas les curés, qui font pousser les orangers.
Ce sont les gens, pas les parasites politiques, pas les commensaux indésirables, pas ce fléau millénaire, qui fait la joie, la connaissance, la poésie et le rythme.
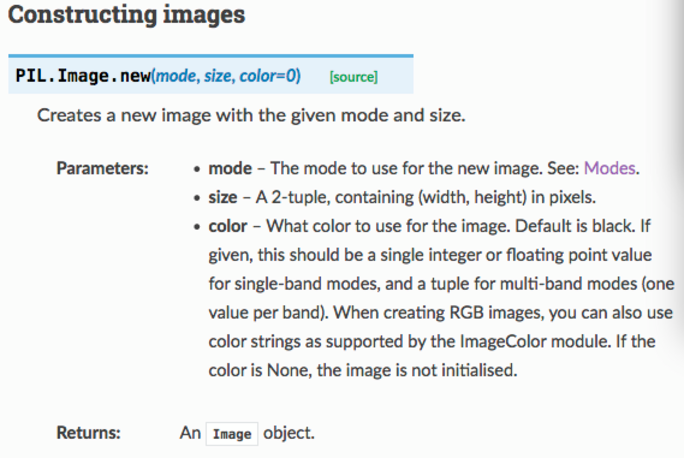
Voici une page de la documentation Pillow, la bibliothèque qui me permet, avec Python, de construire des images. Elle me permet aussi de faire des progrès en anglais (à quelque chose malheur est bon) :
Voici à présent une page du terminal de mon mac, avec lequel il est commode de tester les programmes qu'on écrit. Python est un langage interprété, cela entraîne qu'au débugage, ça s'arrête à chaque bug. C'est pas très joli, je la mets pour les geeks. Ça leur rappellera peut-être bien des prises de tête !
Last login: Thu Dec 5 08:18:58 on console
neurone:~ jean-maxsabatier$ cd desktop
neurone:desktop jean-maxsabatier$ cd python_2019
neurone:python_2019 jean-maxsabatier$ python3 pluz.py
Traceback (most recent call last):
File "pluz.py", line 160, in <module>
approche(diviseurs)
File "pluz.py", line 121, in approche
hachage(points, div[i], domaine, marge)
File "pluz.py", line 100, in hachage
towers.line([sup, mar + dom, sup, p[(i+1)*delta][1]], fill= 0, width=1, joint=None)
NameError: name 'towers' is not defined
neurone:python_2019 jean-maxsabatier$ pluz.py
-bash: pluz.py: command not found
neurone:python_2019 jean-maxsabatier$ python3 pluz.py
Traceback (most recent call last):
File "pluz.py", line 161, in <module>
approche(diviseurs)
File "pluz.py", line 122, in approche
hachage(points, div[i], domaine, marge)
File "pluz.py", line 88, in hachage
towers = ImageDraw.Draw(etape, mode=None)
NameError: name 'etape' is not defined
neurone:python_2019 jean-maxsabatier$ python3 pluz.py
Traceback (most recent call last):
File "pluz.py", line 161, in <module>
approche(diviseurs)
File "pluz.py", line 123, in approche
etape.save(nom, format=None)
NameError: name 'etape' is not defined
neurone:python_2019 jean-maxsabatier$ python3 pluz.py
Traceback (most recent call last):
File "pluz.py", line 162, in <module>
approche(diviseurs)
File "pluz.py", line 124, in approche
hachage(points, div[i], domaine, marge)
File "pluz.py", line 117, in hachage
etape.save(nom, format=None)
NameError: name 'nom' is not defined
neurone:python_2019 jean-maxsabatier$ python3 pluz.py
Traceback (most recent call last):
File "pluz.py", line 162, in <module>
approche(diviseurs)
File "pluz.py", line 124, in approche
hachage(points, div[i], domaine, marge)
File "pluz.py", line 117, in hachage
nom = "courbe" + "_" + str(div[i]) + ".png"
TypeError: 'int' object is not subscriptable
neurone:python_2019 jean-maxsabatier$ python3 pluz.py
neurone:python_2019 jean-maxsabatier$
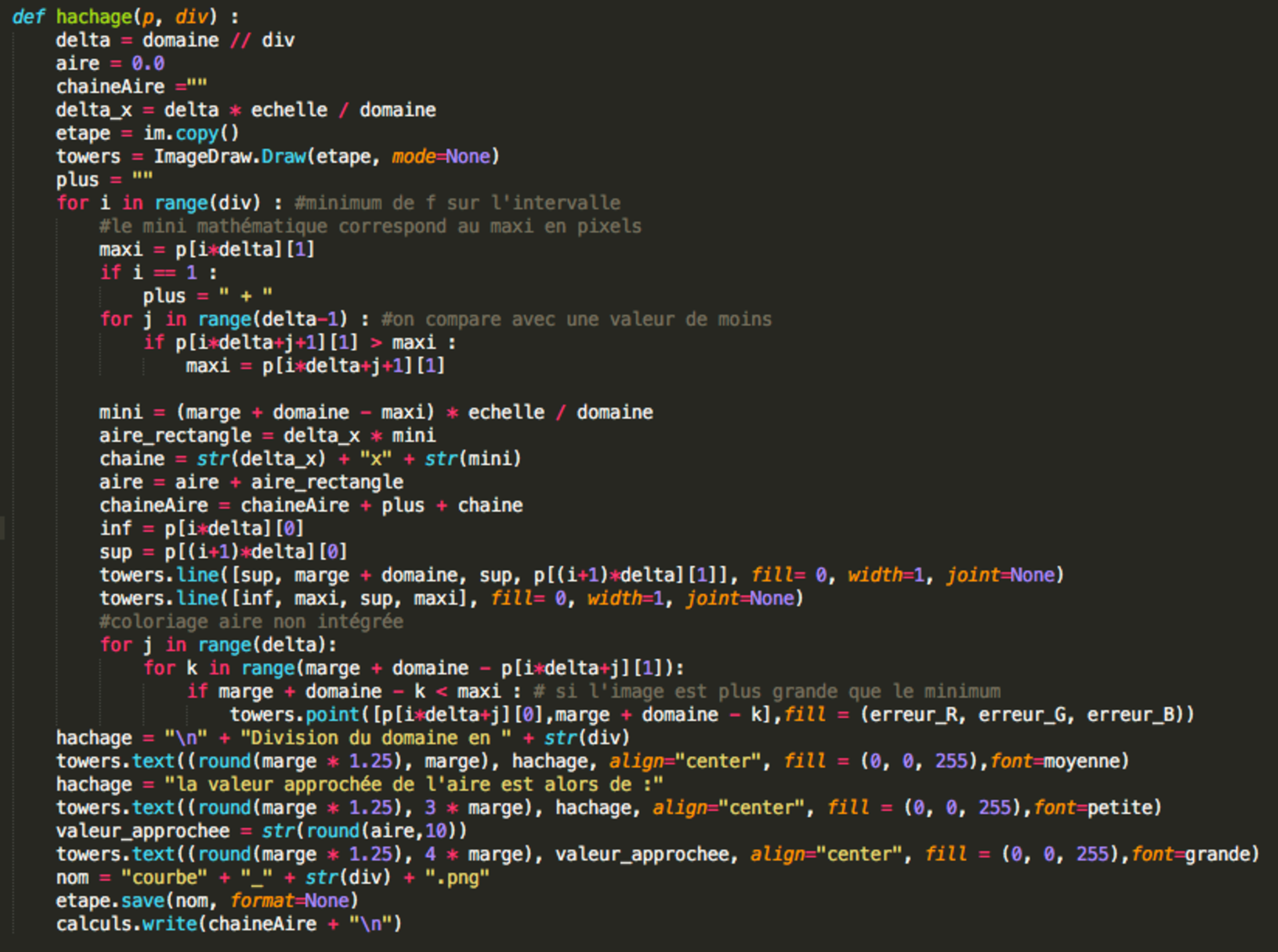
Enfin, on a déjà parlé ensemble de la beauté des mots. Il ne faut pas oublier celle des textes, constitués de mots. En plus de la beauté de ses mots, un texte apporte la beauté de ses idées, de ses structures, de ses rythmes. Eh ben, un programme, c'est beau ! Avec l'éditeur qu'on utilise, qui utilise un code de couleurs pour aider à sa compréhension, c'est même féerique ! Voilà la fonction qui produit une image correspondant à une subdivision du domaine.
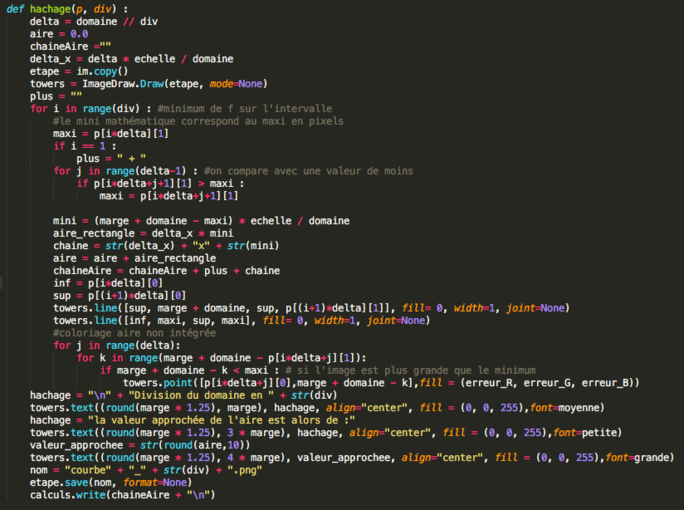
Agrandissement : Illustration 15
Pour finir, quelques petits souvenirs de l'année enfuie, et une photo rigolote.
https://blogs.mediapart.fr/jean-max-sabatier/blog/291018/montez-python
https://blogs.mediapart.fr/jean-max-sabatier/blog/140918/la-librairie-ecole-la-richesse-du-pauvre
Ajouter zéro, sans cesse, au bord du vide

Agrandissement : Illustration 16




